OPTUMG2/Materials
Contents
- 1 STRESS, STRAIN AND SIGN CONVENTIONS
- 2 ELASTICITY
- 3 ELASTOPLASTICITY
- 4 HYDRAULIC MODELS
- 5 COMMON PROPERTIES
- 6 DRAINAGE
- 7 SPATIAL VARIATION OF PARAMETERS
- 8 MOHR-COULOMB
- 9 DRUCKER-PRAGER
- 10 TRESCA
- 11 ANISOTROPIC UNDRAINED SHEAR (AUS)
- 12 HOEK-BROWN
- 13 GSK
- 14 BOLTON
- 15 MODIFIED CAM CLAY
- 16 HARDENING MOHR-COULOMB (HMC)
- 16.1 Typical soil behavior
- 16.2 Model overview
- 16.3 Calibration to Erksak sand
- 16.4 Calibration to Lund sand
- 16.5 Calibrating and
- 16.6 Undrained behavior
- 16.7 Governing equations
- 16.8 Incremental stress-strain relations
- 16.9 Limit Analysis and Strength Reduction
- 16.10 Variational model
- 16.11 Extension to general stress space
- 17 LINEAR ELASTIC
- 18 RIGID
- 19 FLUIDS
- 20 PLATES
- 21 GEOGRIDS
- 22 CONNECTORS
- 23 HINGES
- 24 PILE ROWS
- 25 NAIL ROWS
1 STRESS, STRAIN AND SIGN CONVENTIONS
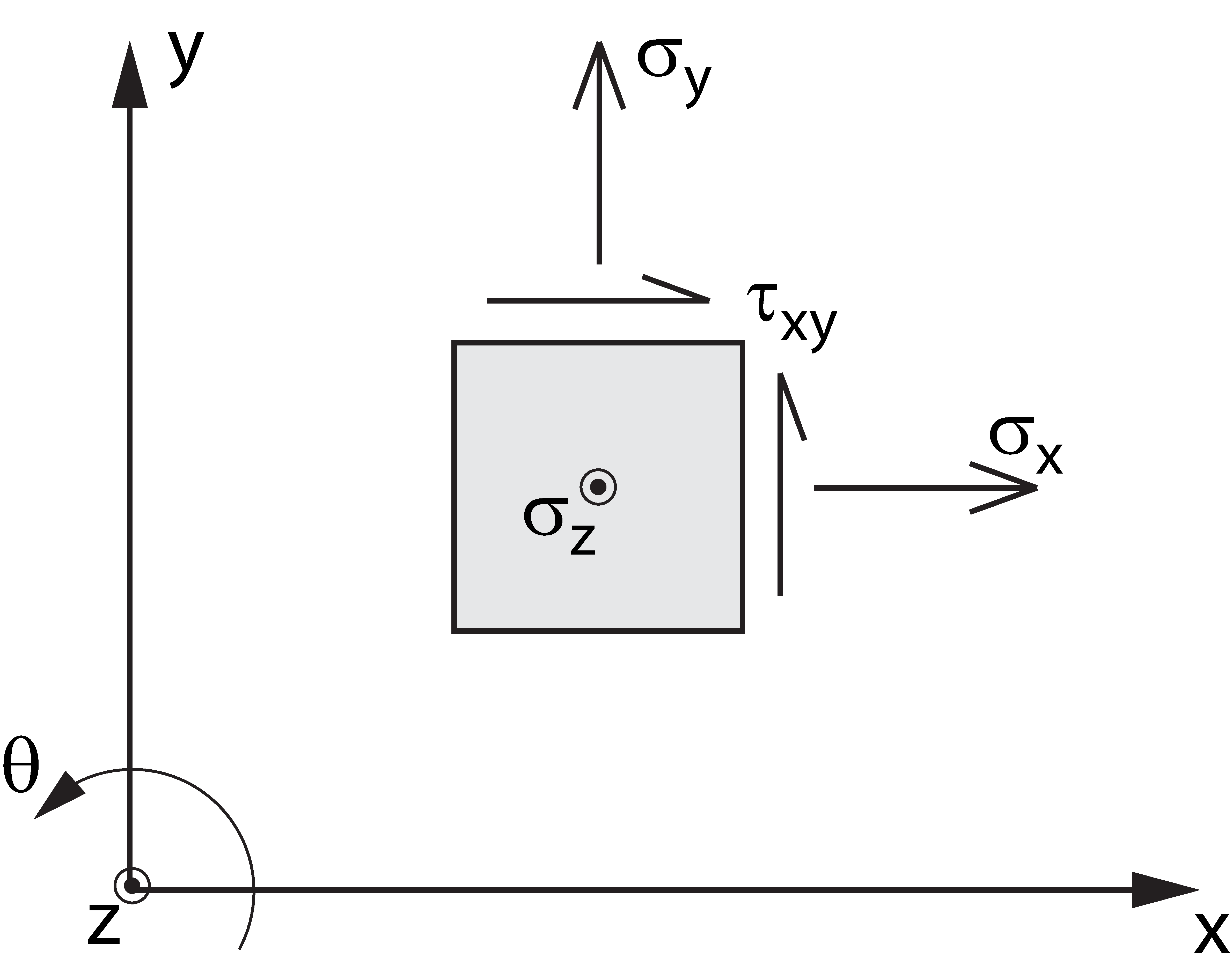
OPTUM G2 makes use of a global Cartesian coordinate system with x and y being the horizontal and vertical axes respectively (see Figure 1). Rotations, , are counted positive counter-clockwise.
The sign conventions used in OPTUM G2 are consistent with those used in most of the solid mechanics literature. Stresses are negative in compression and positive in tension (see Figure 1.1). Similarly, negative normal strains correspond to compaction and positive normal strains correspond to dilation.
OPTUM G2 assumes plane strain conditions. As such, there are four potentially non-zero stress components:
and three potentially non-zero strain components:
However, the theory summarized in the following sections is valid in the general three-dimensional setting.
The principal stresses are ordered as:
That is, is the most compressive principal stress while
is the least compressive. In many cases, the intermediate principle stress,
, will coincide with the out-of-plane stress
.
Similarly, the principal strains are ordered according to:
such that and
are, respectively, the most and least compressive principal strains. Under plane strain conditions, the intermediate principal strain often coincides with the out-of plane strain,
.
 |
1.1 Effective stress
For fluid saturated media, stress-strain relationships are usually formulated with respect to effective stresses. These are related to the total stresses by
where are the effective stresses,
are the total stresses,
is the fluid pressure (negative in compression) and
. The fluid pressures may be given a priori (for example in terms of the hydrostatic pressure distribution underneath the water table) or they may be generated in response to mechanical loading (for example in connection with rapid loading of fine grained materials). The role of pore pressures in soil mechanics is covered in detail in Section 4 of the Theory Manual.
2 ELASTICITY
For elastic materials the strains and effective stresses are related to each other in a one-to-one manner, i.e. the strains generated through loading along one stress path will be recovered when unloading along the same stress path. Assuming linear elasticity, the relation between the strains and the effective stresses can be expressed as:
where is the compliance modulus and
is the stiffness modulus.
2.1 Isotropic elasticity
The most common assumption regarding the stiffness of geomaterials is that of isotropy, i.e. that the properties are the same in all directions, e.g. vertically and horizontally. In this case, the compliance and stiffness moduli, may be expressed either in terms of Young’s modulus and Poisson’s ratio
or in terms of bulk modulus
and shear modulus
. The compliance modulus is given by
or equivalently by:
where
The stiffness modulus is given by:
or equivalently by:
The relations between ,
,
, and
are summarized in the table below.
2.1.1 Undrained conditions
Under undrained conditions, the relation between the elastic strains and the total pressures can be shown to be given by (see the Theory Manual)
where
where
is the undrained Young’s modulus.
This is the elastic law used for the Tresca material (Set A requiring input of and Set B requiring input of
).
2.2 Anisotropic elasticity
As a result of their deposition, natural soils often display cross-anisotropy with the elastic parameters differing between the vertical and horizontal directions. It may be shown that the most general cross-anisotropic elasticity model will involve a total of five parameters. Alternatively, a simplified model that accounts for the basic features of the anisotropy may be used. One such model has been proposed by [Graham:1983]Author: J.~Graham; G.~T.~Houlsby
Journal: Geotechnique
Pages: 165--180
Title: Anisotropic elasticity of a natural clay
Volume: 33
Year: 1983 . In addition to two elasticity parameters this model involves one additional parameter that acts as a measure of the anisotropy. The stress-strain relation of the Graham-Houlsby may be expressed as:
. In addition to two elasticity parameters this model involves one additional parameter that acts as a measure of the anisotropy. The stress-strain relation of the Graham-Houlsby may be expressed as:
where is the Young’s modulus measured in the
-direction,
is the Poisson’s ratio in the
-direction to strain applied in the
-direction, and
is an anisotropy parameter. For thermodynamic consistency, it may be shown that the Poisson’s ratio should be limited to
Alternatively, the above relation may be written as:
where
The anisotropy parameter, , can be related to the Young’s moduli as well as the shear moduli in the different directions:
where and
are the Young’s moduli measured in the two directions,
is the shear modulus in any plane perpendicular to the
-direction and
is the shear modulus in any plane parallel to the
-direction.
3 ELASTOPLASTICITY
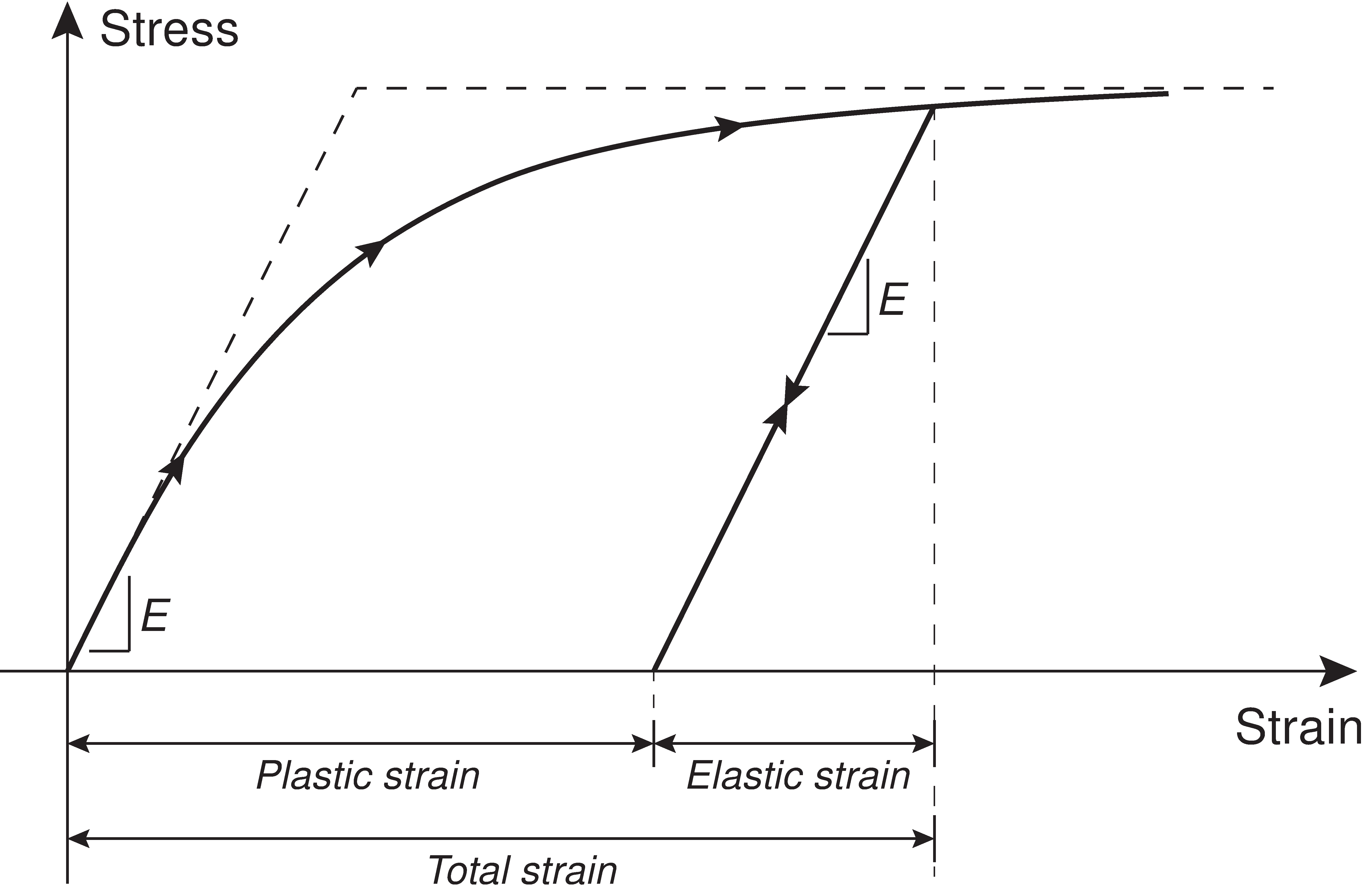
OPTUM G2 makes extensive use of the theory of elastoplasticity in the formulation of constitutive models. In standard laboratory tests such as triaxial compression tests, these models imply an initially elastic response at low levels of loading. This is followed by the accumulation of plastic, or irreversible strains, up to a point where the stress level either asymptotes towards a steady state or - in some cases - drops to a lower level. The typical stress-strain response for an elastoplastic material is shown in Figure 3.1.
 |
In the following, the theory of elastoplasticity will briefly be reviewed before the various material types available in OPTUM G2 will be documented in detail.
3.1 Additive decomposition
The fundamental assumption in elastoplasticity theory is the additive decomposition of elastic and plastic strains (see Figure 3.1):
where are the total strains,
are the elastic strains and
are the plastic strains.
3.2 Elasticity
Assuming linear elasticity, the elastic strains are related to the effective stresses via Hooke’s law:
where is the compliance modulus and
is the stiffness modulus (see Section 2). This law is often stated in incremental form, but holds also in terms of total quantities of effective stress and elastic strain.
3.3 Flow rule
The plastic strains are related to the stresses via a flow rule that usually is expressed as
where is the flow potential,
is a scalar (the so-called plastic multiplier), and a superposed dot indicates incremental quantities.
3.4 Yield function
The stresses are limited by the yield function. This is always a function of the stresses but may also involve various additional variables to account for hardening. The yield function can thus be written as
where are the effective stresses and
is a set of stress-like hardening variables. The yield function is specified such that
corresponds to purely elastic states while
indicates yielding. States leading to
are not permissible under any circumstances. Although many models make use of only one yield function, it is in principle possible to incorporate an arbitrary number into a single model.
3.5 Hardening rule
The evolution of the hardening variable is specified via a hardening rule which in general can be written as
where is the hardening function.
3.6 Complementarity conditions
The plastic multiplier, , must be such that it is non-zero only for stress states corresponding to yielding. This requirement can be expressed via the complementarity conditions:
3.7 Initial stresses
Nonlinear boundary value problems generally require knowledge of the initial state. In geotechnics, the initial stress state is often characterized by the earth pressure coefficient which relates the vertical and horizontal stress components by:
where and
are the horizontal and vertical effective stresses respectively. In OPTUM G2,
is a material parameter which can be used to specify the initial stresses according to the relation above. Furthermore, an additional parameter
can be specified such that the horizontal and vertical stresses can be related by
4 HYDRAULIC MODELS
Variably saturated flow through porous media can be described by the mass balance equation
supplemented with the generalized Darcy’s law
where:
= Porosity
= Degree of saturation
= Fluid velocity [m/day]
= Saturated hydraulic conductivity modulus [m/day]
= Relative hydraulic conductivity which is a function of degree of saturation
= Vertical coordinate
= Unit weight of water (= 9.8 kN/m
)
= Pressure
= Head (=
)
Combining Eq.4.1 and Eq.4.2 leads to what is sometimes (especially in 1D) called Richards equation:
Typical values of hydraulic conductivity for different materials are shown in Figure 4.1.
 |
Besides the constants and
, the solution of this equation requires the relative hydraulic conductivity relation and the saturation-pressure relation (also known as the water retention curve or the soil water characteristic curve).
In OPTUM G2, the saturated hydraulic conductivity modulus is always given by
where and
are the saturated hydraulic conductivities in the
and
directions respectively.
The relative hydraulic conductivity relation and the retention curve are given by one of three available models described below.
4.1 Linear model
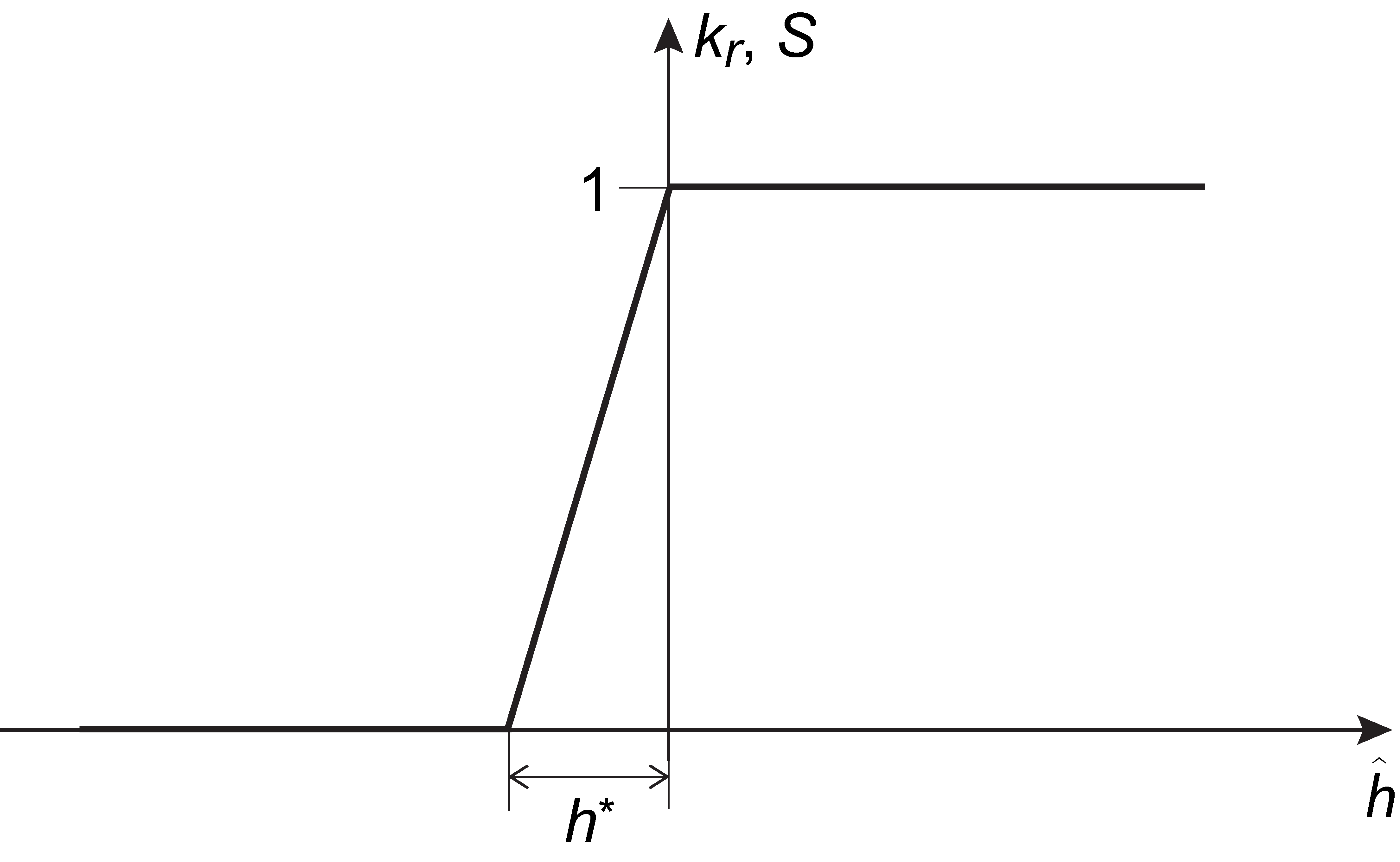
The Linear model is a single-parameter model which approximates the degree of saturation, , by (see Figure 4.2):
where is the pressure head at zero elevation (note that the pore pressure
is negative in the fully saturated range) and
is a material parameter, the default value of which is
m.
 |
The relative hydraulic conductivity is taken simply as the degree of saturation:
4.2 Tanh relative hydraulic conductivity model
The Tanh model is a single-parameter model which approximates the degree of saturation as:
where the parameter specifies the approximate range over which
increases from zero to 1 (see Figure 4.3). The default value of the model parameter is
m.
 |
As with the Linear model, the Tanh model takes the degree of saturation as the relative hydraulic conductivity:
4.3 van Genutchen model
The van Genuchten model is the most widely used hydraulic model in the soil sciences. It relates degree of saturation to pressure head by:
where ,
and:
= Residual degree of saturation (may be slightly greater than 0).
= Fraction of water filled pores at full saturation (may be slightly less than 1).
[m
] = Model parameter related to the air entry pressure.
= Model parameter related to the rate at which water is extracted from the soil once the air entry pressure has been exceeded.
The relative hydraulic conductivity is related to the effective saturation, , as:
where
Alternatively, can be expressed in terms of
as:
Typical values of the parameters and
are given in Table 4.1 and typical retention and relative hydraulic conductivity curves are shown in Figure 4.4.
| Material | No. of | ||||||
| Samples | |||||||
| Sand | 2 | 14 | 18 | 2.22 | 2.56 | 2.74 | 2.65 |
| Loamy sand | 10 | 23 | 108 | 1.33 | 2.56 | 4.41 | 2.35 |
| Sandy loam | 11 | 70 | 178 | 1.12 | 2.38 | 4.90 | 1.27 |
| Sandy clay loam | 15 | 208 | 349 | 1.06 | 1.85 | 3.92 | 1.47 |
| Loam | 7 | 122 | 260 | 1.23 | 1.96 | 4.90 | 1.76 |
| Silt loam | 5 | 120 | 270 | 1.14 | 1.25 | 9.60 | 1.47 |
| Silty clay loam | 8 | 280 | 390 | 1.14 | 1.43 | 8.82 | 0.98 |
| Clay loam | 6 | 304 | 348 | 1.05 | 1.64 | 4.90 | 0.78 |
| Sandy clay | 5 | 352 | 421 | 1.10 | 1.49 | 4.90 | 1.76 |
| Silty clay | 2 | 420 | 460 | 1.09 | 1.10 | 6.37 | 5.39 |
| Clay | 1 | 452 | 452 | 1.51 | 1.51 | 0.88 | 0.88 |
 |
5 COMMON PROPERTIES
The materials available in OPTUM G2 are grouped into six different material categories:
- Solids for the modeling of solid materials (soil, rock, concrete, etc) and interfaces between such materials.
- Fluids for the modeling of bodies of water and other fluids.
- Plates for the modeling of foundation plates, sheet pile walls and other structures that can be idealized as one-dimensional elements in the
-
plane.
- Geogrids for the modeling of geogrids or similar elements that cannot sustain tension.
- Connectors for the modeling of fixed-end anchors and plate-to-plate connections.
- Hinges for the modeling of hinges in Plates.
Each material category contains a one or more material types. For example, the material types within the Solids category include the Mohr-Coulomb, Drucker-Prager, and Hoek-Brown material types. These represent general models and can be further specialized to represent particular materials, for example the Loose Sand-MC, Firm Clay-MC and Loose Sand-HMC materials that are available as predefined materials.
In OPTUM G2, the properties of any material can be gauged either by selecting the geometric object (surface, line, point) to which it has been assigned or by selecting the material in the Materials ribbon. This will bring up a property window located on the right hand side of the canvas. The properties of the material are here organized into a number of different categories, of which Material is common to all materials. Some examples are shown in Figure 5.1.
 |
Material
The Material category contains the following properties:
- Name: the name of the material. This field is editable and any changes will be reflected in the ribbon and throughout the project.
- Category: material category (non-editable).
- Color: Material color. This field is editable and any changes will be reflected in the ribbon and throughout the project.
- Material Type. Examples for Solids include Mohr-Coulomb, Drucker-Prager, and Hoek-Brown.
- Reducible Strength (Yes/No). Determines whether or not the strength parameters of a given material will be reduced in the course of Strength Reduction analysis (see the Analysis Manual).
Besides the common properties, each material type involves a certain number of more specific properties that describe the strength, stiffness, hydraulic conductivity, etc. These will be described in detail for each material type in what follows.
6 DRAINAGE
OPTUM G2 requires that a Drainage condition is specified for each Solid material. There are three possible settings: Drained/Undrained, Always Drained, and Non-Porous. Moreover, for each analysis (each stage), a Time Scope must be chosen. There are two possibilities: Short Term or Long Term. These two settings, Drainage Condition and Time Scope, determine whether the material behaves in a drained or an undrained manner. The basic idea is that some materials behave in a undrained manner in the short term (e.g. clay) while others always behave as drained both in the short term and in the long term (e.g. sand).
The rules for whether a given point in the domain behaves in a drained or an undrained manner are summarized in the table below.
 |
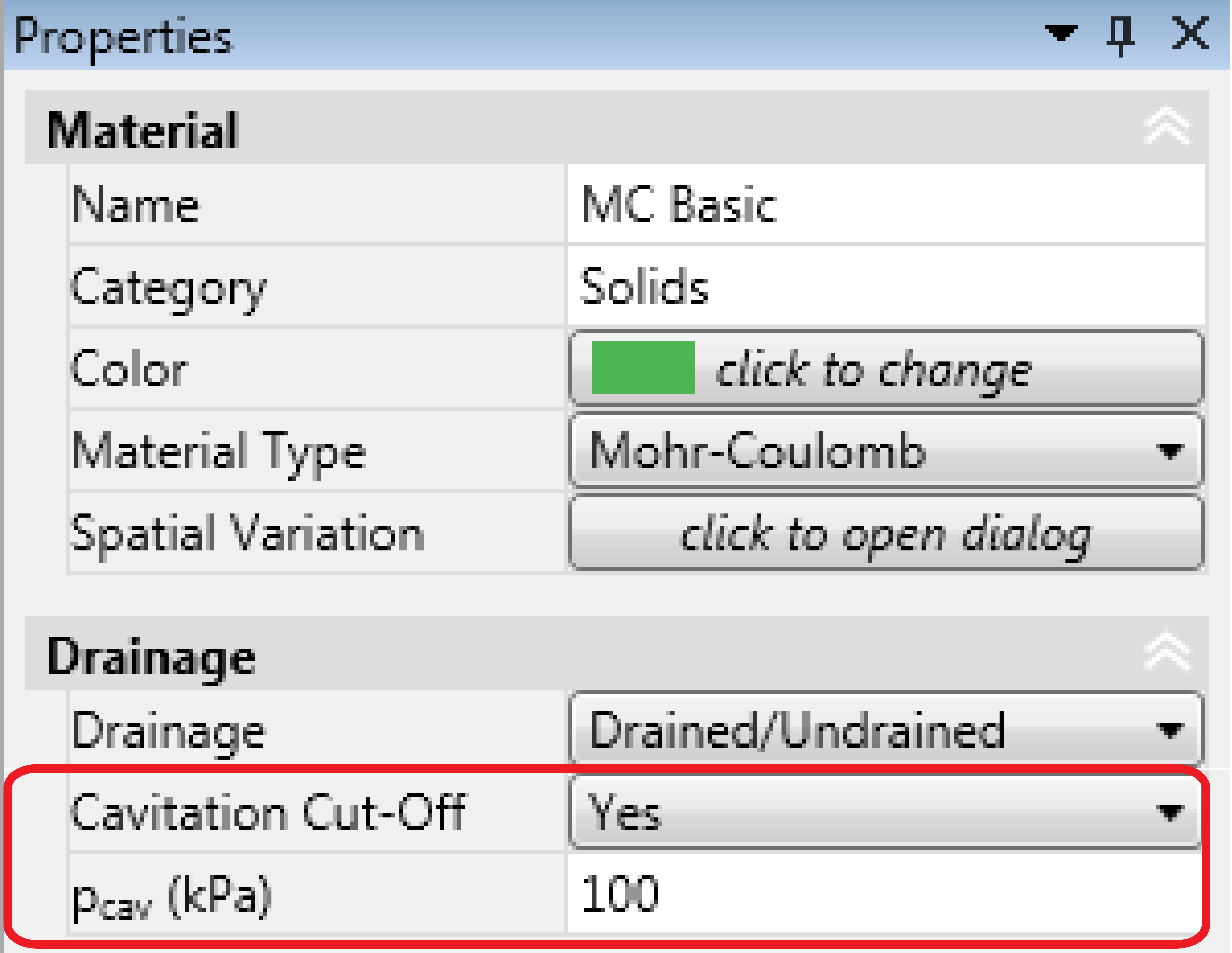
6.1 Cavitation Cut-Off
Under undrained conditions, materials that tend to dilate will produce positive (tensile) excess pore pressures. Under standard conditions, the magnitude of the total pore pressure cannot exceed the atmospheric pressure. This constraint can be imposed via the Cavitation Cut-Off option, see Figure 6.2. Setting Cavitation Cut-Off = Yes, gives the possibility to specify a cavitation pressure, , such that the total pore pressure is limited by
where and
are the seepage and excess pore pressures respectively. Once
, the behaviour becomes effectively drained and volume is no longer preserved. Note that tensile pore pressure are positive consistent with the sign convention adopted for stress and strain.
Cavitation cut-offs are only relevant for Elastoplastic and Multiplier Elastoplastic analysis and are ignored for all other analysis types.
 |
6.2 Relation to “Method A, B, C"
Undrained analysis can be carried out in a number of ways of which the three most common are (see Theory Manual, Section 4):
- Use the original drained parameters – for Mohr-Coulomb
,
,
, and
– in a coupled deformation-excess pore pressure calculation. This is the most general and in many ways the theoretically most satisfactory approach.
- Use drained stiffness parameters and undrained strength parameters – for Mohr-Coulomb
,
, and
– in a coupled deformation-excess pore pressure calculation. This is a rather awkward hybrid approach that generally is not recommended. Note also that even though excess pore pressures are calculated, these are not in general representative of the actual excess pore pressures.
- Use undrained parameters for both stiffness and strength – for Mohr-Coulomb
and
– in which case only a standard deformation analysis without excess pore pressures is necessary.
These three approaches are often referred to as Method A, B and C respectively.
In OPTUM G2, the three different approaches can easily be accommodated. The table below summarizes the relevant settings for a Mohr-Coulomb material with Drainage = Drained/Undrained. It is noted that while undrained analysis according to ‘Method C can be carried out with the Mohr-Coulomb model, the Tresca model caters specifically for this approach. In particular, the use of Tresca allows for the specification of the shear stiffness while the use of Mohr-Coulomb requires that the undrained Young’s modulus be specified (along with a Poisson’s ratio equal to 0.5). Moreover, the use of Tresca allows for a separate partial factor to be applied to the undrained shear strength,
, when using Design Approaches. In conclusion, the recommendations for undrained analysis are:
- Use either the original model, e.g. Mohr-Coulomb, with drained parameters and Time Scope = Short Term (corresponding to Method A), or
- Use the Tresca model with undrained parameters (corresponding to Method C).
Note that while the former approach implies a distribution of undrained shear strength that may or may not be in accordance with what is observed in the field (see Section 8.16.2), the latter approach specifies the distribution of undrained shear strength directly.
 |
7 SPATIAL VARIATION OF PARAMETERS
OPTUM G2 contains a number of options for varying the material parameters spatially. When selecting a material input field in the property grid, two buttons appear on the left: a calculator and a table. Selecting the table opens a window in which the variation of the material parameters can be specified. The following options are available:
- Constant: the trivial option of a constant value of the parameter throughout.
- Gradient: for specifying a linear variation.
- Profile: for specifying the an arbitrary variation with depth via a sequence of points.
- Map: for specifying an arbitrary variation throughout
-
space via a sequence of points.
The three last options are described in below.
7.1 Gradient
The gradient option requires a reference value of the parameter (), two reference points (
and
), two gradients (
and
).
 |
An example is shown above. The resulting distribution of the parameter is here given by
In other words, varies linearly with depth while there is no variation horizontally.
Note that the right-handed coordinate system used in OPTUM G2 implies a negative gradient for parameters that increase with depth. It is strongly advised that spatially varying material parameters be verified by the Material Parameters tool under the Results ribbon.
7.2 Profile
The Profile option offers a flexible way of specifying arbitrary variations of material parameters with depth. This done by specifying points (y, value) in the table under Profile. An example is shown below.
 |
The data may be entered manually or imported from an MS Excel or similar file.
7.3 Map
This is the most general option for defining material data. Data in the form (x, y, value) are specified as shown below.
 |
As for Profile, data may be added manually or imported from an MS Excel file.
7.4 Multiple data sets
For Profile and Map, it is possible to specify multiple data sets for the same material parameter, for example two different profiles which will be processed in the course of two separate analyses.
The specification of multiple data sets is sketched in Figure 7.4. When opening the Material Parameter dialog, Import is clicked and the option Link to data file is selected under Source type. Next, the option Multiple column data is selected under Rows and Columns. Finally, the data file is selected.
The data file is of the same format as standard Profile or Map data files but may contain more than one column of material data (see Figure 7.4).
 |
The linked data option is well suited for parameter studies where the sensitivity of various quantities (bearing capacity, settlement, etc) to the material parameters is sought quantified.
8 MOHR-COULOMB
The Mohr-Coulomb material is a solid material that may be applied both to surfaces and to lines. In the latter case the line will act as a Shear Joint. The Mohr-Coulomb material assumes linear elasticity and a yield function defined by two parameters, cohesion and friction angle. The flow rule is generally nonassociated and defined by a dilation angle and, optionally, a dilation cut-off. In addition, it is possible to specify a tension cut-off and a compression cap. The various parameters can be accessed via the property window. They have been grouped into a number of categories that in the following will be documented in turn.
Material
See Section 5.
Drainage
See Section 6.
Stiffness
The Mohr-Coulomb model offers three different kinds of elasticity: linear isotropic elasticity, nonlinear isotropic elasticity and linear anisotropic elasticity. In the first case, the material parameters can be defined in two ways:
either (Set A):
- Young’s modulus,
[MPa]
- Poisson’s ratio,
or (Set B):
- Bulk modulus,
[MPa]
- Shear Modulus,
[MPa]
The two sets of parameters, and
, are related by
or
It should be noted that the two parameter sets are not linked automatically. For example, if Set A is chosen and and
entered, changing the parameter set to Set B, does not lead to an automatic computation of
and
on the basis of
and
.
Secondly, for the Nonlinear option, the Young’s modulus is pressure dependent following
where
with being the minor principal stress. The associated parameters are:
[kPa] : Reference pressure (confining pressure in triaxial compression test).
: Fitting parameter.
The parameter depends on the soil type. For soft clays,
should be chosen as
(giving rise to relations similar to those used in the Modified Cam Clay model) while for sands and other coarse grained materials
is appropriate.
The final option, Graham-Houlsby, implements the anisotropic elasticity of [[Graham:1983]Author: J.~Graham; G.~T.~Houlsby
Journal: Geotechnique
Pages: 165--180
Title: Anisotropic elasticity of a natural clay
Volume: 33
Year: 1983 see also Section 2.2]. The input parameters are:
see also Section 2.2]. The input parameters are:
- Young’s modulus in the
-direction,
[MPa]
- Poisson’s ratio in the
-direction to strain applied in the
-direction,
- Ratio of the Young’s moduli in the
- and
-directions,
 |
Strength
The basic Mohr-Coulomb yield function is given by
where and
are the major and minor principal stresses respectively and the material parameters are:
- Cohesion,
[kPa]
- Friction angle,
[
]
Some possible depictions of the Mohr-Coulomb yield surface are shown in Figure 8.1.
Flow Rule
 |
The Mohr-Coulomb flow potential is given by
To start with, the Flow Rule category distinguishes between two settings: Associated and Nonassociated. In the former case, is assumed while in the latter case, input of a dilation angle
is required. In addition, for a Nonassociated flow rule, it is possible to specify a Dilation Cap such that the dilation angle is set to zero once the value of a particular strain quantities reaches a critical values. Two different dilation caps, Volumetric and Shear are available. These differ by the strain quantity used to cap the dilation. For Dilation Cap = Volumetric, the dilation angle varies according to [see Figure 8.2(a)]:
where is the volumetric strain. Using a Dilation Cap, a shear strain-volumetric strain behaviour such as that shown schematically in Figure 8.2(b) can be accounted for.
For Dilation Cap = Shear, the dilation angle varies according to [see Figure 8.2(b)]:
where is a measure of the shear (or deviatoric) strain.
In summary, the Flow Rule category involves the following settings and parameters:
- Flow Rule (Associated/Nonassocited)
Flow Rule = Nonassociated: Dilation angle
[
]
Flow Rule = Nonassociated: Dilation Cap (No/Volumetric/Shear) – Dilation Cap = Volumetric:
[%] – Dilation Cap = Shear:
[%]
Tension cut-off (optional)
It is possible to introduce a tension cut-off. This is given by
where the parameters are:
- Tensile strength,
[kPa].
- Inclination of the tension cut-off cone,
[
].
The default values correspond to a regular tension cut-off (,
).
Note: the flow rule used for the tension cut-off is associated. As such, the use of a tension cut-off under undrained conditions may lead to counterintuitive results, including an apparent increase in strength. Hence, the use of tension cut-offs under undrained conditions is not recommended.
 |
Compression Cap (optional)
It is further possible to introduce a compression cap. This is given by
where the cap hardens according to:
where is the part of the plastic volumetric strain associated with the compression cap.
The parameters that define the hardening compression cap are given by:
- Initial compressive strength,
[kPa].
- Inclination of the compression cone,
[
].
- Hardening (Yes/No)
Hardening = Yes: Hardening parameter,
[kPa].
The flow potential of the compression cap is the cap yield function, i.e. flow on the cap is associated.
The Mohr-Coulomb yield functions are shown in Figure 8.4. Alternatively, in terms of the normal and shear stresses on the critical plane, the yield functions take on the appearance shown in Figure 8.5.
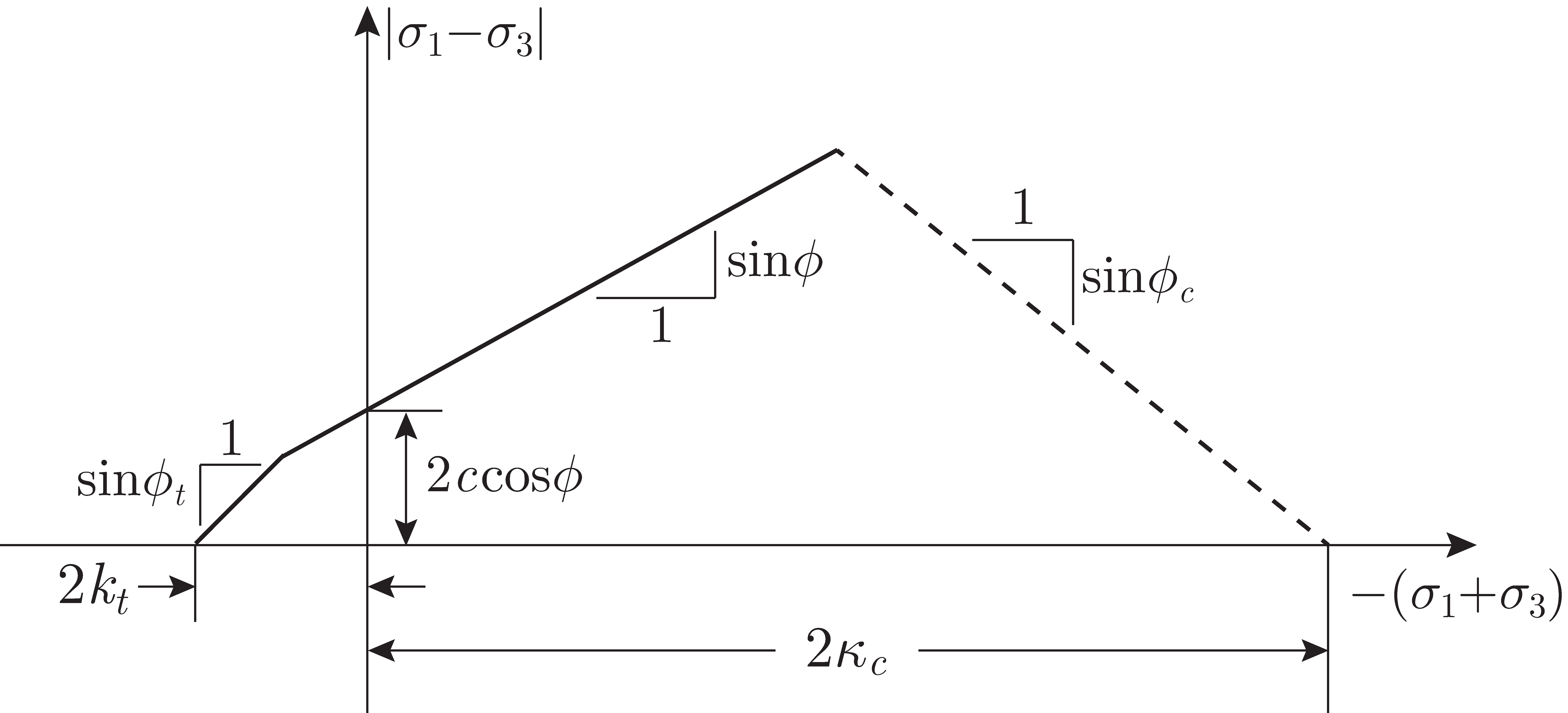 |
 |
For confined compression under drained conditions, the compression cap implies a bilinear stress-strain response as shown in Figure 8.6.
 |
Under undrained conditions, the stress path (for ) is as shown in Figure 8.7. The undrained shear strength,
, depends on both the elastic and plastic parameters and is given by
where
and ,
, and
are the initial effective stresses and hardening variable respectively. From Eq.8.12 the following limits of
are obtained:
 |
An example of the influence of the ratio is shown in Figure 8.8.
 |
Fissures (optional)
 |
The strength of materials with regular fissure patterns may be accounted for by using a combination of the usual Mohr-Coulomb failure criterion supplemented with additional constraints on the normal and shear stresses on the fissure planes [Davis:1980]Author: E.~H.~Davis
Booktitle: Proc. 3rd A.N.Z. Conf. on Geomechanics, vol. 3. Wellington, New Zealand
Pages: 27--36
Title: Some plasticity solutions relevant to the bearing capacity of rock and fissured clay
Year: 1980 , [Zheng:1997]Author: Z.~Zheng; J.~R.~Booker; J.~P.~Carter
, [Zheng:1997]Author: Z.~Zheng; J.~R.~Booker; J.~P.~Carter
Journal: International Journal of Solids and Structures
Pages: 1211--1243
Title: Limit analysis of the bearing capacity of Fissured materials
Volume: 37
Year: 1997 . In OPTUM G2, it is possible to define two fissure planes such that the strength is limited by:
. In OPTUM G2, it is possible to define two fissure planes such that the strength is limited by:
where is the usual Mohr-Coulomb yield function Eq.8.5 and
and
are the normal and shear stresses on the two fissure planes. In OPTUM G2, up to two fissure planes (not necessarily mutually orthogonal) can be defined via the following parameters:
- Orientation of Plane
,
[
].
- Cohesion on Plane
,
[kPa].
- Friction angle on Plane
,
[
].
- Tensile strength of Plane
,
[kPa].
where and the angles
are as shown in Figure 8.9. Note: setting
implies that the constraint
is ignored.
Unit weights
The weight of the materials is specified via:
- Dry unit weight,
[kN/m
].
- Saturated unit weight,
[kN/m
].
For calculations involving seepage or stationary water tables, the unit weight at any given point is calculated as:
where is the degree of saturation.
Initial Conditions
The initial stresses are specified via two parameters:
- The earth pressure coefficient
.
- The parameter
(kPa).
The Initial Stress analysis aims to determine an admissible stress field that satisfies:
For , we have the classic relations
Hydraulic Model
The hydraulic properties of the materials are specified via:
- Hydraulic model (Linear, van Genuchten, Tanh).
- Hydraulic conductivity in the
direction,
[m/day].
- Hydraulic conductivity in the
direction,
[m/day].
- Parameters related to the particular hydraulic model (see Section 4 for details).
8.1 Notes
Dilation Cap: The dilation angle is updated at the beginning of each load step or each new stage. As such, for Dilation Cap = Volumetric, the total volumetric strain at the end of the load or stage may in calculations be observed to be somewhat higher than , especially locally around footing edges and other singularities.
Dilation in Short Term analysis the dilation angle may affect the results significantly and an inadequate choice of dilation angle may lead to unexpected and counterintuitive results. In particular, for Drained/Undrained materials under Short Term analysis, any other value than will lead to an infinite limit load (see the Theory manual). Consequently,
is automatically set to zero for such analyses.
8.2 Influence of dilation angle on limit load
In the analysis types Limit Analysis and Strength Reduction under Long Term conditions, the dilation angle is always assumed associated, i.e. a user defined dilation angle that differs from the friction angle will be overridden for these analysis types. On the other hand, for Elastoplastic and Multiplier Elastoplastic analysis the user specified dilation angle will be used. The question then arises as to what extent the dilation angle affects the limit load. While the full answer to this question is rather involved and multifaceted, it is indisputable that the limit load for a material with will be greater than or equal to that a material with
. The extent to which the assumption of nonassociated flow reduces the bearing capacity is quite problem dependent. A reasonable estimate of the reduction can be obtained by conducting the limit analysis using a set of reduced parameters that depend on the original
,
, and
as:
where are the original parameters and
are the reduced parameters [often referred to as Davis parameters after [Davis:1968]Address: Butterworth, London
Author: E.~H.~Davis
Booktitle: Soil Mechanics: Selected Topics
Editor: I.~K.~Lee
Pages: 341--380
Title: Theories of plasticity and the failure of soil masses
Year: 1968 who first proposed them]. The strength reduction factor
who first proposed them]. The strength reduction factor and the corresponding friction angle
are tabulated below for different
and
.
| 5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1.0000 | 1.0038 | 1.0154 | 1.0353 | 1.0642 | 1.1034 | 1.1547 | 1.2208 | 1.3054 | 1.4142 | |
| 5 |
– | 1.0000 | 1.0039 | 1.0158 | 1.0364 | 1.0668 | 1.1086 | 1.1642 | 1.2370 | 1.3321 |
| 10 |
– | – | 1.0000 | 1.0040 | 1.0164 | 1.0382 | 1.0707 | 1.1161 | 1.1776 | 1.2597 |
| 15 |
– | – | – | 1.0000 | 1.0042 | 1.0174 | 1.0407 | 1.0762 | 1.1266 | 1.1962 |
| 20 |
– | – | – | – | 1.0000 | 1.0045 | 1.0187 | 1.0443 | 1.0838 | 1.1410 |
| 25 |
– | – | – | – | – | 1.0000 | 1.0048 | 1.0205 | 1.0491 | 1.0941 |
| 30 |
– | – | – | – | – | – | 1.0000 | 1.0054 | 1.0229 | 1.0556 |
| 35 |
– | – | – | – | – | – | – | 1.0000 | 1.0061 | 1.0262 |
| 40 |
– | – | – | – | – | – | – | – | 1.0000 | 1.0070 |
| 45 |
– | – | – | – | – | – | – | – | – | 1.0000 |
| 5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 4.98 | 9.85 | 14.51 | 18.88 | 22.91 | 26.57 | 29.84 | 32.73 | 35.26 | |
| 5 |
– | 5.00 | 9.96 | 14.78 | 19.35 | 23.61 | 27.51 | 31.03 | 34.15 | 36.89 |
| 10 |
– | – | 10.00 | 14.94 | 19.70 | 24.19 | 28.33 | 32.10 | 35.47 | 38.44 |
| 15 |
– | – | – | 15.00 | 19.92 | 24.62 | 29.02 | 33.05 | 36.68 | 39.90 |
| 20 |
– | – | – | – | 20.00 | 24.90 | 29.54 | 33.84 | 37.75 | 41.23 |
| 25 |
– | – | – | – | – | 25.00 | 29.88 | 34.46 | 38.65 | 42.43 |
| 30 |
– | – | – | – | – | – | 30.00 | 34.86 | 39.36 | 43.45 |
| 35 |
– | – | – | – | – | – | – | 35.00 | 39.83 | 44.26 |
| 40 |
– | – | – | – | – | – | – | – | 40.00 | 44.80 |
| 45 |
– | – | – | – | – | – | – | – | – | 45.00 |
It should be noted that while the Davis parameters usually lead to a bearing capacity less than that obtained in an elastoplastic analysis with the actual ,
and
, there are also cases where the opposite is true (see the Example Manual).
8.3 Strength reduction
In Strength Reduction analysis, the Mohr-Coulomb criterion is treated by reducing the parameters and
equally (see Figure 8.10) to induce a state of collapse. The resulting factor is the strength based factor of safety:
While the decision as to which parameters are reduced is quite subjective, the approach used in OPTUM G2 is very common and may further be viewed as being consistent with Eurocode 7. It does, however, suffer from the drawback that the tensile strength, , is unaffected by the reduction, i.e.
.
 |
8.4 Capabilities and limitations of Mohr-Coulomb
The Mohr-Coulomb model has a number of inherent limitations and cannot be expected to capture the entire spectrum of soil behaviour. On the other hand, as with any model, the predictions of the Mohr-Coulomb model depend crucially on the choice material parameters. Generally speaking, if the material parameters are reasonable, so are the predictions of the model.
Moreover, it should be recognized that while more complex models may lead to better predictions for some particular stress paths or types of laboratory experiments, there is no guarantee that the predictions under different conditions represent reality any better than a simpler model. Indeed, while the limitations of the Mohr-Coulomb model are well known, the same is often not the case for more complex models where the predictions under conditions for which the model has not be calibrated may be quite erroneous.
As such, while the relative simplicity of the Mohr-Coulomb model imposes certain limitations, it is the same simplicity and transparency that makes it an attractive tool for practical geotechnical analysis.
In the following, two well known limitations of the Mohr-Coulomb model are briefly discussed.
8.4.1 Initial stiffness versus unloading/reloading stiffness
For real soils, one often observes that the stiffness in unloading/reloading is significantly higher than in initial (virgin) loading. The Mohr-Coulomb model, however, operates with a single elastic stiffness in both regimes. This means that the real soil stiffness is either underestimated in unloading/realoading (if the elastic parameters are set to match the soil response in first loading), or overestimated in first loading (if the elastic parameters are set to match the soil response in unloading/reloading. This point is illustrated in Figure 8.11.
 |
Consequently, some care must be exercised in the choice of Young’s modulus. For example, for a footing loaded for the first time, the initial secant modulus, , would be appropriate while for excavation problems, the unloading/reloading modulus,
, may be more representative of the actual soil stiffness. As a general rule of thumb, the two moduli are related by
–
. It should be noted, however, that many problems will be dominated by effects other than those related to the elastic moduli of the soil. For example, the deformation of retaining structures in excavation problems may be much more dependent on the soil strength and the properties of the retaining system (walls, anchors, etc) than the soil stiffness moduli. Also, the ultimate limit state is independent of the elastic properties of the soil.
The shortcomings of the Mohr-Coulomb model in capturing the different moduli in initial loading and unloading/reloading are addressed by the Extended Mohr-Coulomb (HMC) model described in Section 16.
8.4.2 Undrained conditions
Under undrained conditions (in OPTUM G2, for materials with Drainage Conditions = Drained/Undrained in analyses with Time Scope = Short Term), the Mohr-Coulomb model, with , implies a zero change of effective mean stress. Assuming plane strain conditions, it may be shown that the sum of the in-plane effective stresses remains constant. This sum can further be identified as the sum of the major and minor effective stresses. The Mohr-Coulomb yield function may therefore be written as:
where is the initial effective vertical stress (positive in compression) and
is the initial earth pressure coefficient. Under undrained conditions, the Mohr-Coulomb failure criterion thus reduces to that of Tresca (see Section 10) with a cohesion equal to the undrained shear strength
.
The stress path under undrained plane strain conditions is illustrated in Figure 8.12. The shear stress is here increased under an initial effective pressure
.
In other words, the undrained shear stress is a function of the initial vertical effective stress, the earth pressure coefficient, and the Mohr-Coulomb parameters and
.
The conditions under general stress states, including those encountered in axisymmetry, are considerably more complex than those in plane strain. They are covered in detail in Section 10.
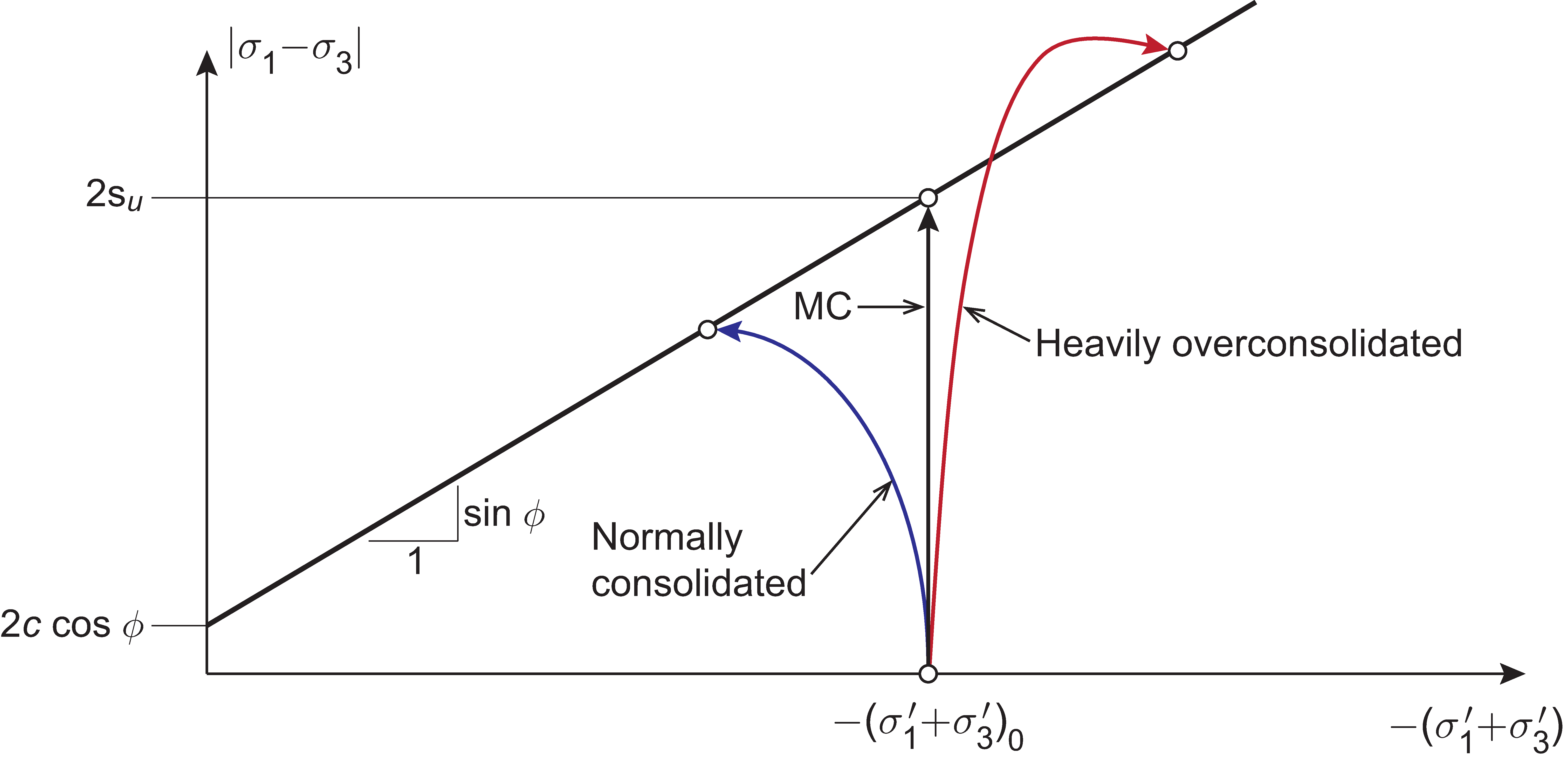 |
The predicted behaviour of the Mohr-Coulomb model and its implications in terms of strength are an approximation to real soil behaviour. Generally speaking, some changes to the mean effective stress will occur when soils are sheared under undrained conditions. Normally consolidated soils will tend to contract, leading to an increase in excess pore pressure and thereby a decrease in effective mean stress with the result that the maximum shear stress is lower than predicted by the Mohr-Coulomb model. On the other and, heavily overconsolidated soils will tend to dilate, leading to a decrease in excess pore pressure and thereby an increase in effective mean stress and hence a higher maximum shear stress than predicted by the Mohr-Coulomb model. The former type of behaviour may to some extent be accounted for by a hardening cap. Otherwise, if sufficient material data is available, the Modified Cam Clay model is well suited to capture the behaviour of soft soils under undrained conditions.
9 DRUCKER-PRAGER
The Drucker-Prager material is very similar to the Mohr-Coulomb material but uses slightly different expressions for the yield and plastic potential function.
Material, Drainage, Stiffness
See Section 8
Strength
The Drucker-Prager yield function is given by
where
The strength parameters of the Drucker-Prager model are:
- Friction coefficient
.
- Cohesion
[kPa].
Flow Rule
The Drucker-Prager flow potential is given by
The settings in the flow rule category are analogous to those of the Mohr-Coulomb material with and
replacing
and
respectively.
Tension cut-off (optional)
It is possible to introduce a tension cut-off of the type:
where the parameters are:
- Slope of tension cut-off
.
- Tensile strength
[kPa].
Note that the default value corresponds to a plane strain Mohr-Coulomb friction angle of
(see Section 9.9)
Compression Cap (optional)
It is further possible to introduce a compression cap. This is given by
where the cap hardens according to:
with being the part of the plastic volumetric strain associated with the compression cap.
The parameters that define the hardening compression cap are given by:
- Initial compressive strength,
[kPa].
- Slope of the compression cone,
.
- Hardening (Yes/No).
Hardening = Yes: Hardening parameter,
[kPa].
The flow potential of the compression cap is the cap yield function, i.e. flow on the cap is associated. The Drucker-Prager yield function and compression cap are shown in Figure 9.1.
 |
Unit weights, Initial Stresses, Permeability
See Section 8.
9.1 Notes
Dilation Cap: See Section 8.12.
9.2 Influence of dilation on limit load
The effects of nonassociated flow on the limit load are similar to those described for the Mohr-Coulomb model (see Section 8.13). For the Drucker-Prager model the equivalent Davis parameters are given by [see [Krabbenhoft:2012IJNME]Author: K.~Krabbenhoft; M.~R.~Karim; A.~V.~Lyamin; S.~W.~Sloan
Journal: International Journal for Numerical Methods in Engineering
Pages: 1089--1117
Title: Associated computational plasticity schemes for nonassocited frictional materials
Volume: 89
Year: 2012 for details]:
for details]:
where
In other words, use of and
in place of the original parameters will in Limit Analysis and Strength Reduction lead to results similar to those of a full nonassociated elastoplastic calculation to failure using the original
,
and
.
9.3 Drucker-Prager vs Mohr-Coulomb
Assuming associated flow, the Drucker-Prager and Mohr-Coulomb surfaces can be matched in plane strain (see Figure 9.2) by the following choice of parameters:
where and
are the Mohr-Coulomb parameters. The equivalent
and
are tabulated as function of
and
in Table 9.1). In Limit Analysis and other analyses using an associated flow rule, the Drucker-Prager model with the equivalent Mohr-Coulomb parameters will produce results identical to the Mohr-Coulomb model. However, in elastoplastic calculations, the Drucker-Prager model will lead to a slightly less stiff response than the Mohr-Coulomb model.
In the general nonassociated case, the Drucker-Prager dilation coefficient can be matched approximately to the Mohr-Coulomb dilation angle by
In drained elastoplastic analysis using a nonassociated flow rule, it is often observed that the Drucker-Prager model with equivalent Mohr-Coulomb parameters leads to a lower bearing capacity for a given mesh. However, as the mesh is refined, the two models will eventually result in similar bearing capacities.
 |
| 0 | 1.732051 | 0.000000 | |||
| 1 | 1.731699 | 0.030226 | 26 | 1.509171 | 0.736071 |
| 2 | 1.730644 | 0.060435 | 27 | 1.492839 | 0.760639 |
| 3 | 1.728888 | 0.090607 | 28 | 1.476049 | 0.784829 |
| 4 | 1.726432 | 0.120723 | 29 | 1.458816 | 0.808635 |
| 5 | 1.723279 | 0.150767 | 30 | 1.441153 | 0.832050 |
| 6 | 1.719434 | 0.180719 | 31 | 1.423074 | 0.855069 |
| 7 | 1.714900 | 0.210563 | 32 | 1.404594 | 0.877687 |
| 8 | 1.709684 | 0.240280 | 33 | 1.385726 | 0.899901 |
| 9 | 1.703791 | 0.269854 | 34 | 1.366484 | 0.921705 |
| 10 | 1.697228 | 0.299267 | 35 | 1.346881 | 0.943096 |
| 11 | 1.690004 | 0.328503 | 36 | 1.326932 | 0.964073 |
| 12 | 1.682125 | 0.357546 | 37 | 1.306650 | 0.984631 |
| 13 | 1.673602 | 0.386381 | 38 | 1.286046 | 1.004769 |
| 14 | 1.664444 | 0.414992 | 39 | 1.265135 | 1.024486 |
| 15 | 1.654661 | 0.443365 | 40 | 1.243929 | 1.043781 |
| 16 | 1.644263 | 0.471484 | 41 | 1.222440 | 1.062651 |
| 17 | 1.633262 | 0.499338 | 42 | 1.200681 | 1.081098 |
| 18 | 1.621671 | 0.526912 | 43 | 1.178662 | 1.099120 |
| 19 | 1.609499 | 0.554195 | 44 | 1.156396 | 1.116718 |
| 20 | 1.596762 | 0.581173 | 45 | 1.133893 | 1.133893 |
| 21 | 1.583470 | 0.607837 | 46 | 1.111165 | 1.150645 |
| 22 | 1.569637 | 0.634174 | 47 | 1.088221 | 1.166974 |
| 23 | 1.555277 | 0.660176 | 48 | 1.065073 | 1.182883 |
| 24 | 1.540404 | 0.685832 | 49 | 1.041730 | 1.198373 |
| 25 | 1.525030 | 0.711133 | 50 | 1.018201 | 1.213445 |
9.4 Strength reduction
In Strength Reduction analysis (see the Analysis Manual), the Drucker-Prager criterion is treated by reducing the parameters and
equally (see Figure 9.3) to induce a state of collapse. The resulting factor is the strength based factor of safety:
 |
While the decision as to which parameters are reduced is quite subjective, the approach used for the Drucker-Prager criterion is consistent with the one used for the Mohr-Coulomb criterion. As such, the tensile strength, , is unaffected by the reduction.
9.5 Undrained conditions
Under undrained conditions with , the effective mean stress remains constant and the Drucker-Prager yield function can be expressed as
where
is the undrained strength. The Drucker-Prager yield condition thus effectively reduces to that of von Mises.
10 TRESCA
As discussed in Section 8.16.2, the effective stress Mohr-Coulomb model is equivalent to the Tresca model under undrained conditions in plane strain. Under more general stress states than those associated with plane strain, this consistency between the effective stress Mohr-Coulomb model and total stress Tresca model is lost.
The Tresca material model addresses this issue by providing two models: the Standard Tresca model involving the yield function Eq.8.21 and the Generalized Tresca model involving a similar total stress yield function consistent with the effective stress Mohr-Coulomb model under general stress states.
Unlike most solid materials, the Tresca material does not require input regarding drainage and no excess pore pressures are calculated regardless of the the Time Scope.
Material
See Section 8.
Stiffness
The Tresca model operates with undrained elastic parameters: (Set A) or
(Set B).
Strength
Two options regarding strength are available:
- Standard, requiring input of the undrained shear strength,
(kPa).
- Generalized, requiring input of the undrained shear strengths in triaxial compression and triaxial extension,
and
(kPa), respectively.
These two options are discussed in more detail below.
Spatial variation the strength parameters may be specified as for all other materials.
Tension cut-off, Unit Weights, Initial Conditions, Hydraulic Model
See Section 8.
10.1 Standard Tresca
The Standard Tresca failure criterion is given by
with being the undrained shear strength. In plane strain, there is no ambiguity about the physical meaning of
, it is the undrained shear strength measured in direct simple shear or similar plane strain experiments. For full consistency with the Mohr-Coulomb model, the undrained shear strength should be set to:
where it is assumed that the initial effective stresses are related by . However, the idea with the Tresca model, is that
instead is specified directly, without reference to other parameters, and possibly made to increase with depth to reflect the expected dependence on the initial vertical stress.
10.2 Generalized Tresca
While the Standard Tresca model in it itself is quite general, its use under any other conditions than plane strain is somewhat unsatisfactory. Firstly, the fundamental soil parameters are those which govern the response of effective stress versus strain. As such, any total stress model should, as a minimum, be equivalent to a relevant underlying effective stress model. This equivalence exists between Mohr-Coulomb and Standard Tresca in plane strain, but not under more general stress states. Secondly, it is a well established experimental fact that the undrained strength shear is a function of the stress path leading to failure. For example, undrained shear strengths measured in triaxial compression and triaxial extension may differ considerably. However, the Standard Tresca model predicts equal undrained shear strengths regardless of the stress path or type of experiment.
The Generalized Tresca model addresses these shortcomings of the standard model by using the following yield function:
where compressive stresses are negative and the principal stresses are ordered as . Consistency with the Mohr-Coulomb model in terms of the strength domain is obtained by selecting the parameters
and
as:
where it is assumed that the initial effective stresses are related by (in axisymmetry by
).
Alternatively, the parameters and
can be related to the undrained shear strengths measured in triaxial compression and triaxial extension:
where is the undrained shear strength measured in triaxial compression and
is the undrained shear strength measured in triaxial extension. These parameters,
and
, are those required as input in OPTUM G2. As with all other parameters,
and
can be made to increase with depth to reflect dependence on the initial effective vertical stress. The Generalized Tresca yield surface is shown in Figure 10.1. It should be noted that the allowable parameter range is
Outside this range the yield surface becomes non-convex and the calculation will not proceed.
 |
10.3 Theoretical and empirical relations for undrained shear strength
For plane strain Short Term analysis with Drained/Undrained Mohr-Coulomb materials, the equivalent Tresca undrained shear strength parameter is given by
where and
are the Mohr-Coulomb parameters,
is the earth pressure coefficient, and
is the initial vertical effective stresses (positive in compression). The implied variation of
with
and
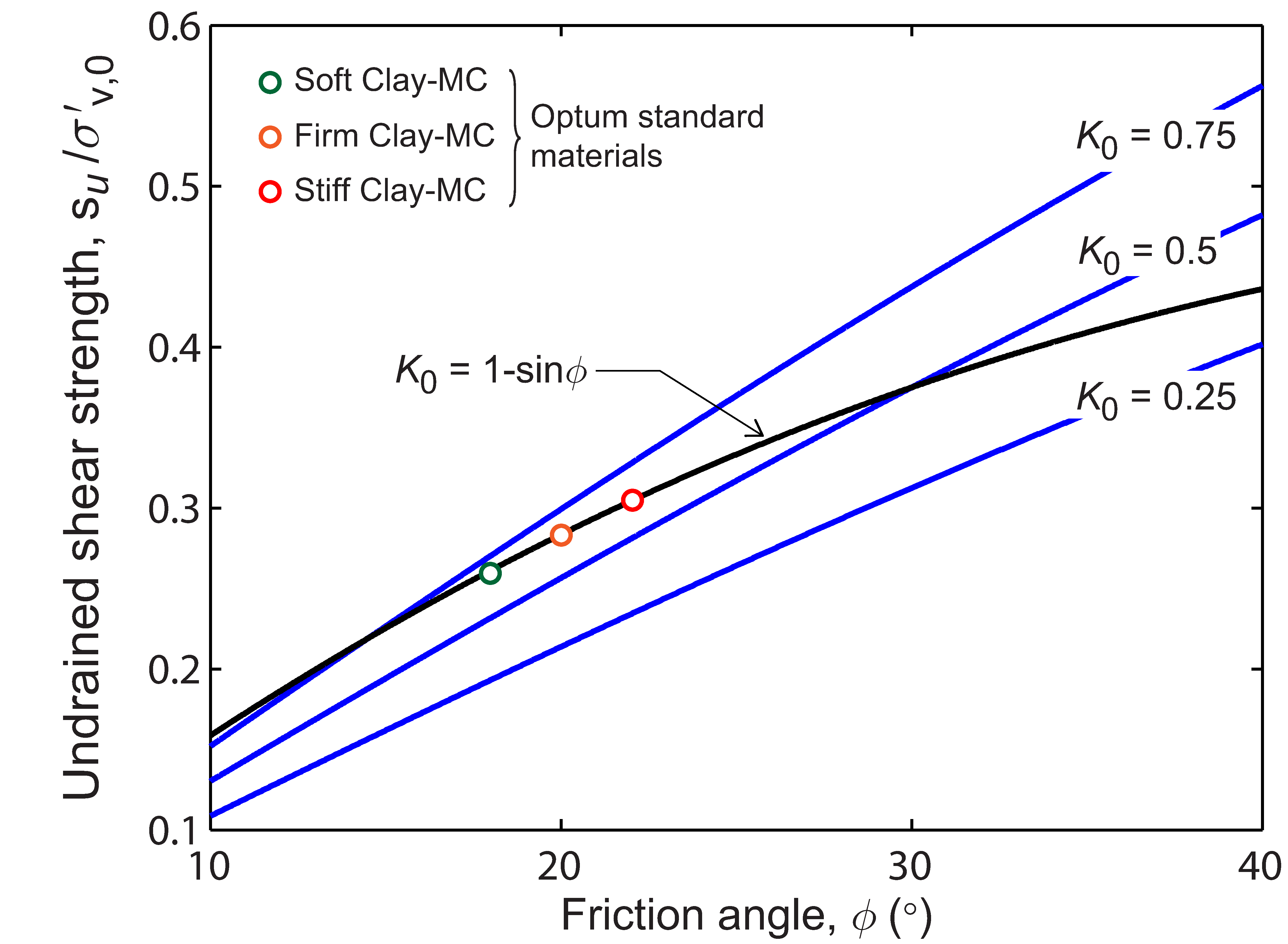
is shown in Figure 10.2. We see that for realistic values of the drained parameters, the implied
ratio is in the range of about 0.1 to 0.5. This corresponds fairly well to what is observed experimentally for normally consolidated clays (see Figure 10.3).
 |
 |
Moreover, a large number of empirical relations for the ratio are available, some of which are summarized in Table 10.1. A detailed discussion of these and similar relations are given by [Wood:1990]Author: D.~{Muir~Wood}
Publisher: Cambridge University Press
Title: Soil Behaviour and Critical State Soil Mechanics
Year: 1990 and [Ladd:2003]Author: C.~C.~Ladd; D.~J.~{D}e{G}root
and [Ladd:2003]Author: C.~C.~Ladd; D.~J.~{D}e{G}root
Booktitle: Proceedings of the 12th Panamerican Conference on Soil Mechanics and Geotechnical Engineering, Cambridge, MA
Pages: 1--60
Title: Recommended practice for soft ground site characterization: {A}rthur {C}asagrande {L}ecture
Volume: 1
Year: 2003 .
.
| Normally consolidated clays [Skempton:1957]Author: A.~.W.~Skempton Journal: Proceedings of the Institution of Civil Engineers London Pages: 305--307 Title: Discussion: The planning and design of the new {H}ong {K}ong airport Volume: 7 Year: 1957 
| |
| Clays with Journal: Journal of the Geotechnical Engineering Division Pages: 409--412 Title: Discussion of "{N}ew design procedure for stability of soft clays" by {L}add, {C. C.} and {F}oott, {R.} Volume: 101 Year: 1975 
| |
| Soft inorganic clays with Journal: Canadian Geotechnical Journal Pages: 591--602 Title: Undrained shear strength in stability calculation of embankments and foundations on soft clays Volume: 17 Year: 1980 
| |
| Inorganic clays [Ladd:2003]Author: C.~C.~Ladd; D.~J.~{D}e{G}root Booktitle: Proceedings of the 12th Panamerican Conference on Soil Mechanics and Geotechnical Engineering, Cambridge, MA Pages: 1--60 Title: Recommended practice for soft ground site characterization: {A}rthur {C}asagrande {L}ecture Volume: 1 Year: 2003 
| |
| Silts and organic soils not including peats [Ladd:2003]Author: C.~C.~Ladd; D.~J.~{D}e{G}root Booktitle: Proceedings of the 12th Panamerican Conference on Soil Mechanics and Geotechnical Engineering, Cambridge, MA Pages: 1--60 Title: Recommended practice for soft ground site characterization: {A}rthur {C}asagrande {L}ecture Volume: 1 Year: 2003 
| |
| Clays with Journal: Soils and Foundations Pages: 1--12 Title: Shear modulus and shear strength of cohesive soils Volume: 14 Year: 1974 
| |
| Stiff clays [Vardenega:2011]Author: P.~J.~Vardanega; M.~D.~Bolton Journal: Canadian Geotechnical Journal Pages: 1485--1503 Title: Strength mobilization in clays and silts Volume: 2048 Year: 2011 
|
Concerning the ratio between the triaxial compression and extension strengths, the effective stress Mohr-Coulomb model predicts:
where is the drained friction angle. By correlating this ratio to the plasticity index, for example by [Wood:1990]Author: D.~{Muir~Wood}
Publisher: Cambridge University Press
Title: Soil Behaviour and Critical State Soil Mechanics
Year: 1990 :
:
we have
The implied variation of the ratio with the plasticity index is shown in Figure 10.4. The available data tend to confirm a trend of this kind although the scatter in the data is significant. Further details on the modeling of arbitrary
ratios are covered under the AUS model in Section 11.
 |
10.4 Strength Reduction
In Strength Reduction analysis, the strengths are reduced to produce a state of incipient collapse. The Factor of Safety is thus defined by
In practice, however, it is usually more convenient to conduct the analysis as a Limit Analysis with Multiplier = Gravity. If only Tresca materials are present, the resulting gravity multiplier, i.e. gravity based factor of safety, is equal to the strength based factor of safety:
In contract to Strength Reduction, Limit Analysis requires only a single iteration and is therefore usually considerably faster.
11 ANISOTROPIC UNDRAINED SHEAR (AUS)
The Anisotropic Undrained Shear (AUS) model may be seen as a further development of the Generalized Tresca model described in Section 10.6. It is a total stress model aimed at clays and similar materials. The input parameters comprise material data that can be easily determined in standard undrained laboratory tests. The particular features of the AUS model include:
- A hardening Generalized Tresca yield surface. This yield surface is consistent with the behaviour of frictional materials, including clays, under undrained conditions and general stress states.
- Direct specification of the undrained shear strengths in triaxial compression, triaxial extension, and simple shear.
- Distinction between elastoplastic secant stiffnesses in triaxial compression and extension.
Being a total stress model, the AUS model does not require input regarding drainage and no excess pore pressures are calculated regardless of the Time Scope.
Material
See Section 8.
Stiffness
The AUS model operates with standard isotropic elasticity, with input parameters being either the undrained Young’s modulus, (Set A), or the shear modulus,
(Set B).
In addition to the elastic stiffnesses, the axial strains halfway to failure in compression and extension are required :
- Axial strain at half the failure stress in triaxial compression,
[%]
- Axial strain at half the failure stress in triaxial extension,
[%]
These quantities are shown in Figure 11.1.
Strength
The strength may be either Isotropic or Anisotropic. In both cases, the undrained shear strengths in triaxial compression and extension are the basic strength parameters (see discussion below). The full set of material parameters is:
- Undrained shear strength in triaxial compression,
[kPa]
- Undrained shear strength in triaxial extension,
[kPa]
- Undrained shear strength in simple shear,
(for Option = Anisotropic)
Spatial variation of the strength parameters may be specified as for all other materials.
Tension cut-off, Unit Weights, Initial Conditions, Hydraulic Model
See Section 8.
11.1 Background
The typical behaviour of clays and similar materials in undrained triaxial compression and extension is roughly as sketched in Figure 11.1.
 |
In the triaxial compression test, an initial state given by is first established. The axial stress is then increased by an amount
until failure is reached at
.
In the triaxial extension test, the same initial state is used, but the axial stress is now released by an amount until failure is reached at
.
The failure strengths in the two cases, measured by half the difference in axial and radial stress are the undrained shear strengths, and
, respectively.
The following general observations hold over a wide range of conditions:
- The compression strength,
, is usually larger than the extension strength,
. In the field, both strengths tend to vary approximately linearly with the vertical stress and thereby approximately linearly with depth.
- The response is usually, but not always, somewhat stiffer in compression than in extension. In OPTUM G2, the overall elastoplastic stiffness is specified via the elastoplastic moduli in compression and extension,
and
respectively.
 |
11.2 Undrained shear strengths
It is usually observed that the undrained shear strengths in triaxial compression (), triaxial extension (
) and simple shear (
) are related to each other by
The phenomenon that the undrained shear strengths resulting from different types of loading differ from one another is often referred to as anisotropy. This is somewhat unfortunate as anisotropy usually refers to the phenomenon that a material has different properties in different directions. For example, as a result of their deposition, many soils have a lower hydraulic conductivity vertically than horizontally. Similarly, some soils may have different elastic properties in the different directions, for example a higher Young’s modulus vertically than horizontally.
It is also possible to contemplate that some soils would have anisotropic strengths, e.g. one strength when subjected to compression vertically and another when subjected to the same kind of compression horizontally. However, the fact that different undrained shear strengths result from different types of loading is not, in the first instance, an indication of anisotropy in the usual sense of the word. It is an entirely expected feature of any frictional material (including clays, silts and similar) whose drained strengths differ in compression and extension (see Figure 11.2).
These observations must necessarily enter into the considerations when developing a reasonable constitutive model and the AUS model is unique in this regard. In particular, it distinguishes sharply between the part of the and
ratios that would be expected from an isotropic material and the part than could reasonably be conceived as stemming from physical anisotropy, for example as a result of layering, direction of deposition, etc.
Moreover, the AUS model provides the option of including physical anisotropy or not. If physical anisotropy is not included, and
are the basic strength parameters and
follows from these. If physical anisotropy is included, there is the additional possibility of specifying the
ratio (within certain limits).
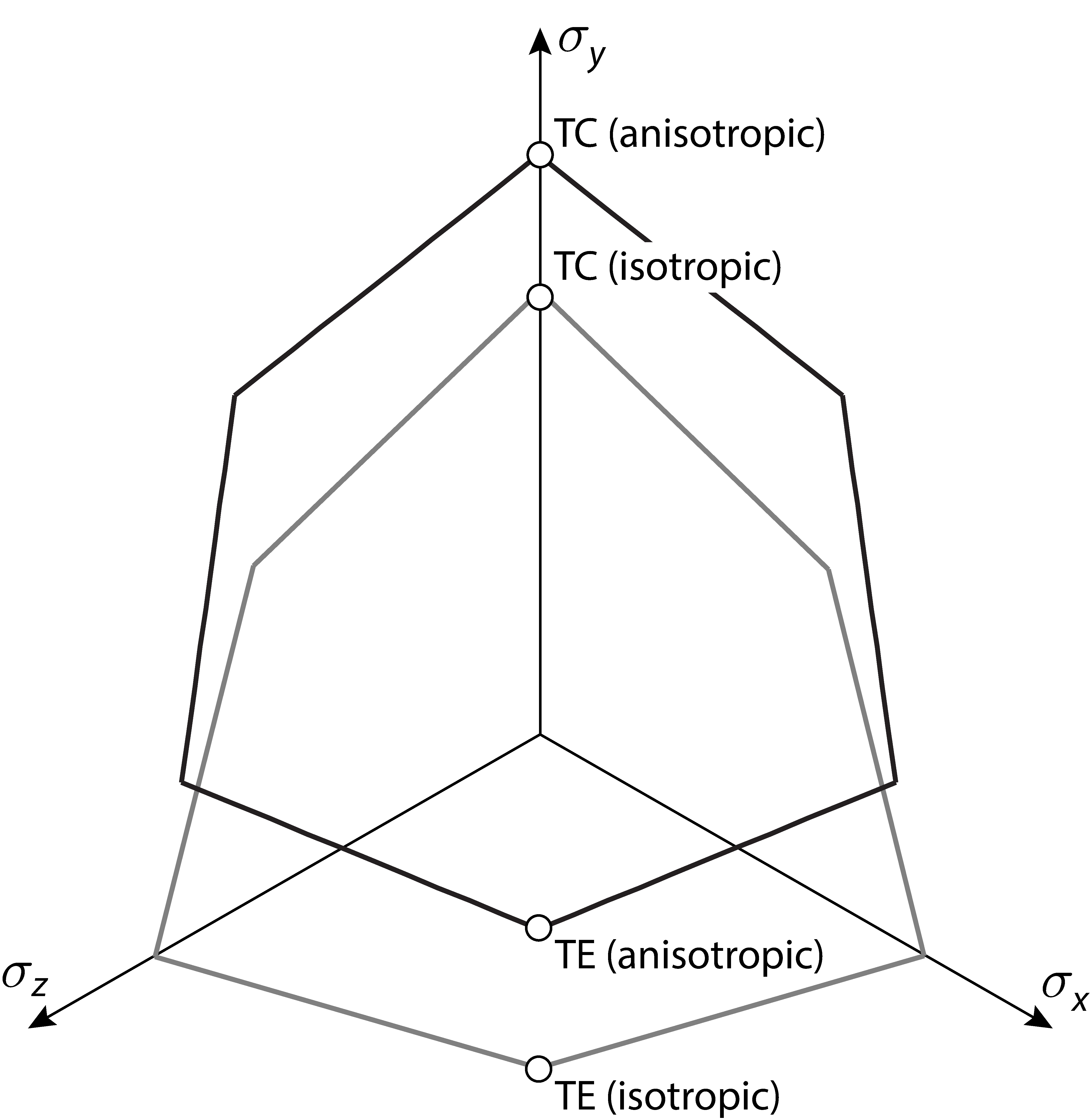
11.2.1 Isotropic strength
For the Isotropic strength option, the Generalized Tresca surface is used (see Figure 11.3) and the triaxial compression and extension strengths are the basic strength parameters. This model comes with the limitation that
For below 0.5 the yield surface becomes non-convex and while ratios of
up to 2 in principle could be accommodated, the internal limitation in OPTUM G2 is that the compression strength remains greater than or equal to the extension strength.
 |
With and
specified, the strength in simple shear follows as:
In other words, is the harmonic mean of the triaxial extension and compression strengths. This means that
will tend to be somewhat closer to
than to
, something that is generally observed experimentally.
 |
11.2.2 Anisotropic strength
The Anisotropic strength option allows for specification of in addition to
and
. To ultimately achieve the desired strengths (if they do not comply with the Isotropic predictions outlined above) the shape of the yield surface is altered and it is shifted in the
-direction (thereby identifying this direction with the orientation of the samples in the tests from which the strengths are determined). The basic principle is illustrated in Figure 11.4.
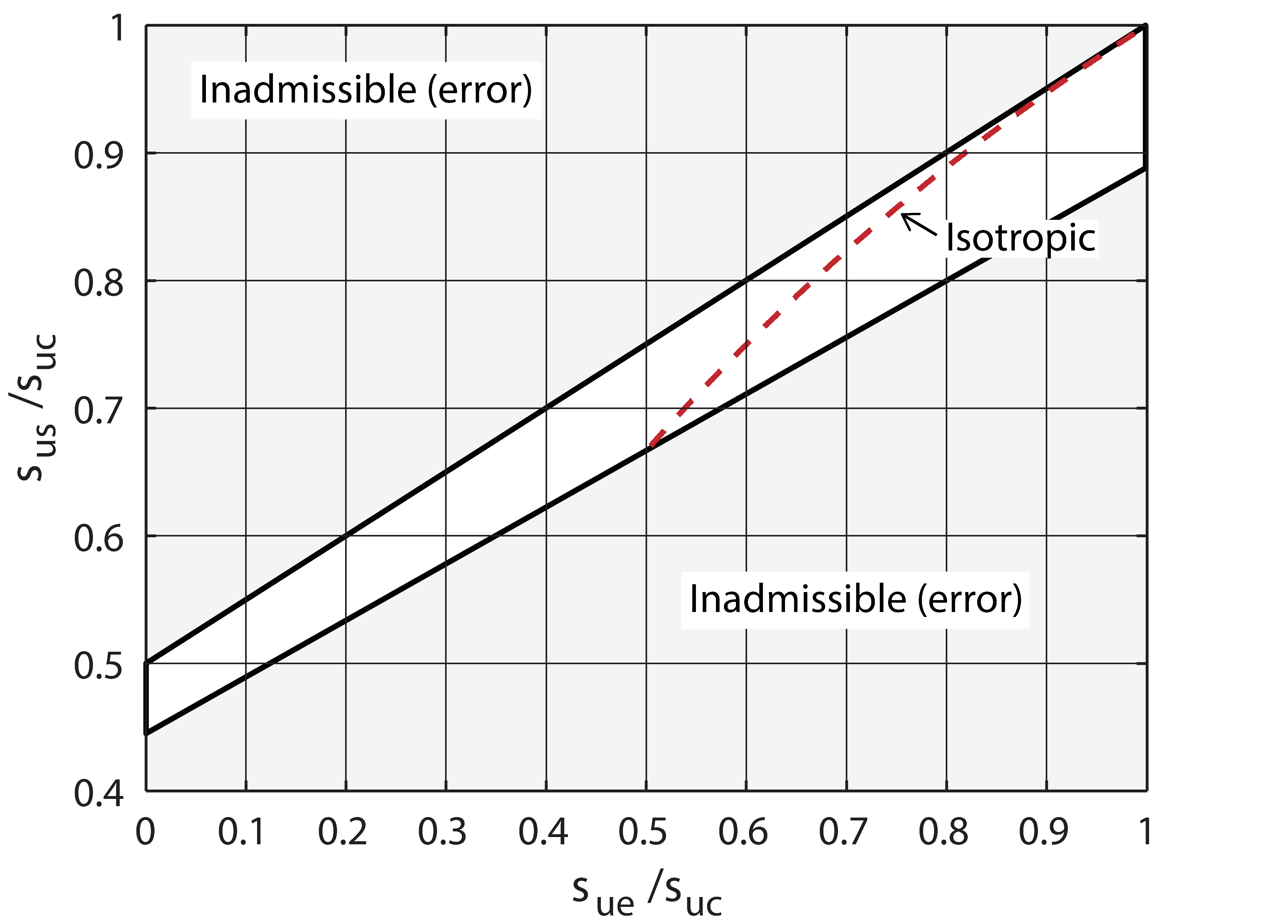
It should be noted, however, that constraints pertaining to the convexity of the yield surface prevent a completely arbitrary ratio from being specified. In particular, for a given
ratio there is an upper and a lower limit to the
ratio that can be accommodated, namely:
These limits are illustrated in Figure 11.5. For ratios outside the admissible range, an error will be issued and the calculations will not proceed.
A unique feature of the Anisotropic version of the AUS model is that anisotropy only is included to the extent that it is necessary to accommodate the specified strength ratios. If the parameters are specified according to the relations implied by the Isotropic version, no anisotropy will result. More generally, the degree of anisotropy eventually included is a function of how much the specified strength ratios differ from what would be expected from an isotropic material.
 |
 |
11.3 Hardening
With the shape and shift of the yield surface in place, the model is completed by specifying an appropriate hardening law. In the AUS model the hardening is of the isotropic kind, meaning that from an initial yield surface that contains the initial stress state, the yield surface expands in an affine manner as a result of plastic straining to reach its ultimate extent as given by the strength parameters. This is illustrated in Figure 11.6.
11.4 Plastic potential
The plastic potential of the AUS model is that of von Mises, i.e. a circle in the deviatoric plane. This type of plastic potential has long been used for clays [see e.g. [Roscoe:1968]Author: K.~H.~Roscoe; J.~B.~Burland
Booktitle: Engineering Plasticity
Editor: J.~Heyman and F.~A.~Leckie
Pages: 535--609
Publisher: Cambridge University Press
Title: On the generalized stress-strain behaviour of wet clay
Year: 1968 , [Potts:2001]Author: D.~M.~Potts; L.~Zdravkovic
, [Potts:2001]Author: D.~M.~Potts; L.~Zdravkovic
Publisher: Thomas Telford
Title: Finite Elements Analysis in Geotechnical Engineering
Year: 2001 ] and has a number of advantages over the immediate alternatives such as Tresca.
] and has a number of advantages over the immediate alternatives such as Tresca.
11.5 Parameter estimation
11.5.1 Strengths
Ideally speaking, the three different shear strengths should be determined in three independent experiments. If only data from one or two experiments are available, the remaining parameters can be estimated on the basis of previously published results. A data set involving all three strengths is that of [Ladd:1991]Author: C.~C.~Ladd
Journal: Journal of Geotechnical Engineering
Pages: 540--615
Title: Stability evaluation during staged construction
Volume: 117
Year: 1991 shown in Figure 11.7.
shown in Figure 11.7.
 |
From this data set, the following approximate relations can be inferred:
and thereby:
for .
In another study concerned with Norwegian clays, [Karlsrud:2013]Author: K.~Karlsrud; F.~G.~Hernandez-Martinez
Journal: Canadian Geotechnical Journal
Pages: 1273--1293
Title: Strength and deformation properties of Norwegian clays from laboratory tests on high-quality block samples1
Volume: 50
Year: 2013 linked the strength ratio to the water content
linked the strength ratio to the water content :
and thereby:
for (corresponding to the range of water contents considered,
% to
).
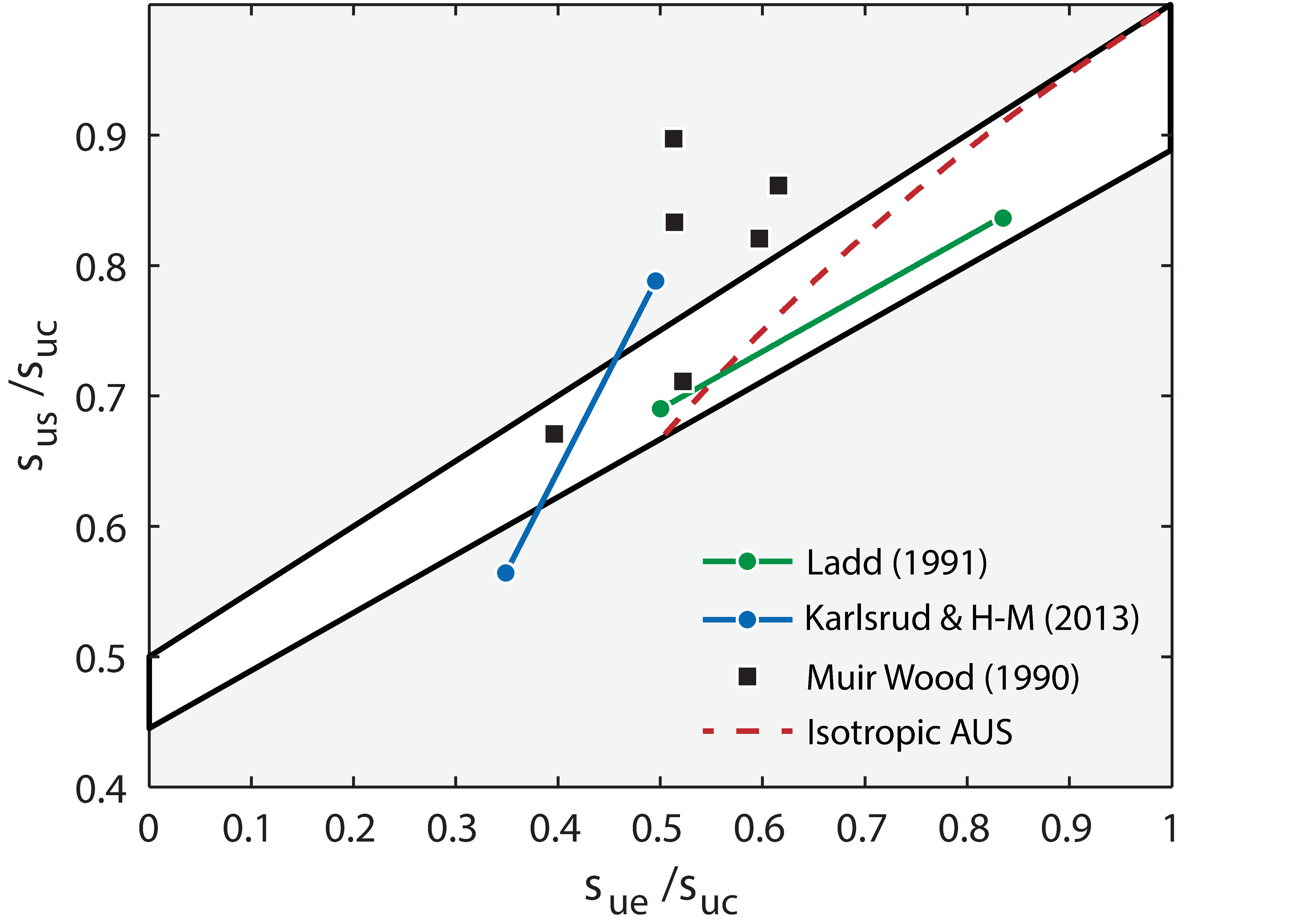
This above relations are shown in Figure 11.8 together with the minimum and maximum that are attainable with the AUS model. Also shown are various data collected by [Wood:1990]Author: D.~{Muir~Wood}
Publisher: Cambridge University Press
Title: Soil Behaviour and Critical State Soil Mechanics
Year: 1990 . We see that the AUS model is capable of accommodating most of these experimentally determined shear strength ratios.
. We see that the AUS model is capable of accommodating most of these experimentally determined shear strength ratios.
 |
11.5.2 Strains halfway to failure
The axial strain halfway to failure in triaxial compression is usually of order to 2% over a wide range of conditions. The strain at halfway to failure in extension is usually some 2 to 5 times
.
11.5.3 Example
Figure 11.9 shows the results of a triaxial compression test on Todi clay reported by [Burland:1996]Author: J.~B.~Burland; S.~Rampello; V.~N.~Georgiannou; G.~Calabresi
Journal: Geotechnique
Pages: 491--514
Title: A laboratory study of the strength of four stiff clays
Volume: 146
Year: 1996 . The test was conducted under a confining pressure of
. The test was conducted under a confining pressure of kPa.
From the test data shown in Figure 11.9, the undrained shear strength is immediately read off as:
The axial strain at this level of is approximately
. A secant modulus can thus be defined by
Using an elastic modulus 10 times this, MPa, results in the fit shown in Figure 11.9. The remaining parameters (which have no influence on the behaviour in compression) must either be estimated or derived from an additional extension test.
 |
11.6 Governing equations
The governing equations of the AUS model are summarized below.
The yield function is given by
where is a hardening variable and
This produces the a rounded version of the Generalized Tresca surface with a shift in the -direction of magnitude
. In the general anisotropic case,
,
and
may be related to the three undrained shear strengths,
,
and
by
The flow rule is given by
The hardening rule is given by
where is the plastic multiplier and
with and
being the axial strains (in percent) halfway to failure in triaxial compression and extension respectively.
11.7 Notes
11.7.1 Limit analysis
Limit analysis is available for the AUS model as for all other models. Since iterations are required the results are somewhat influenced by the convergence tolerance which can be set under Convergence Parameters in Project. Moreover, since the AUS model is nonassociated (Generalized Tresca for the yield potential and von Mises for the flow potential) a situation may arise where where limit loads calculated with the Lower element are slightly larger than those calculated with the Upper element. However, in far most cases the difference between the two will be very small and the situation is in fact an indication that the solution is unlikely to change significantly upon further mesh refinement.
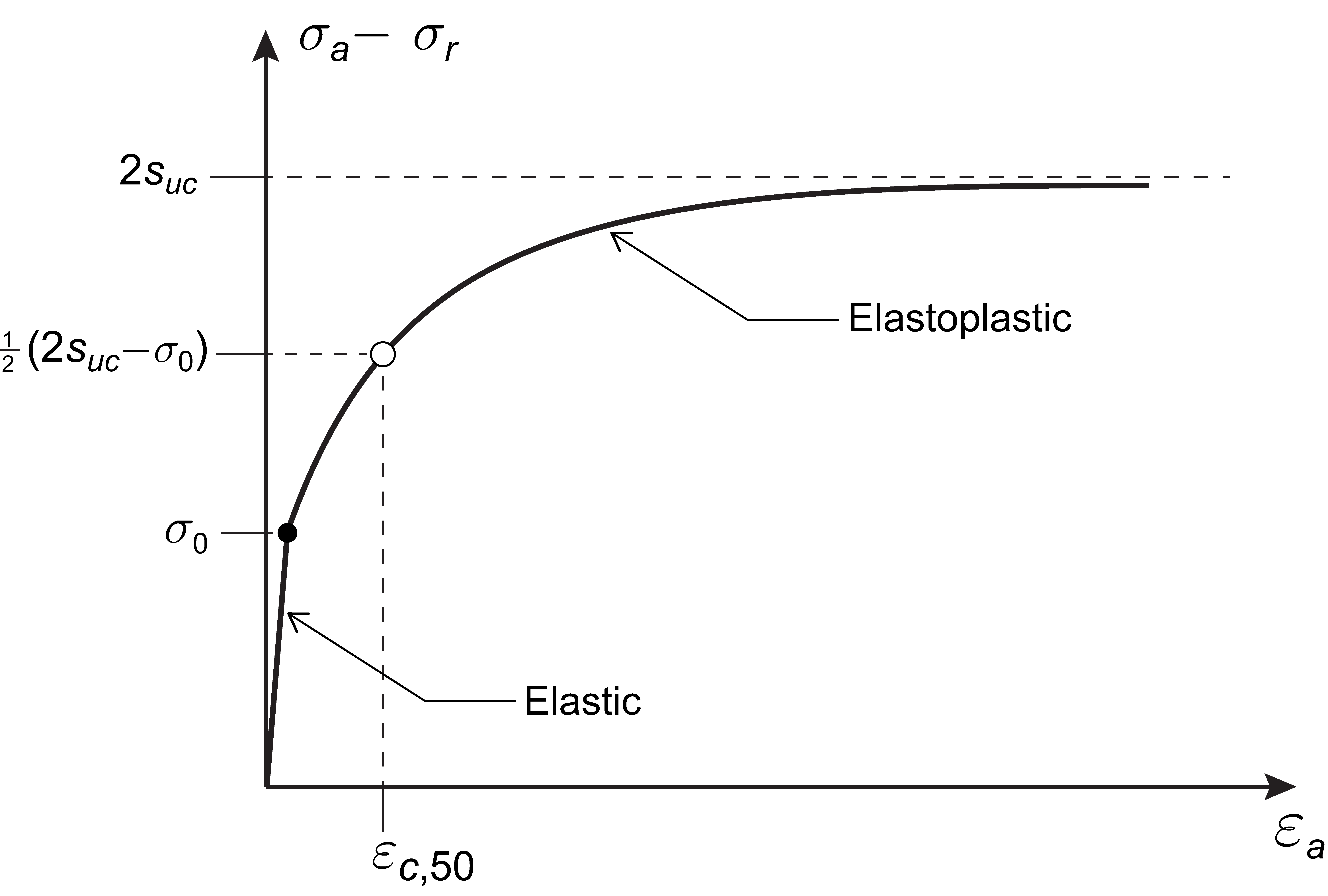
11.7.2 Strains halfway to failure
Strictly speaking, the input material parameters and
refer to the the plastic strains halfway to failure in compression and extension. Usually, the distinction between total and plastic strains is immaterial as the elastic strains will be an order of magnitude smaller than the plastic strains. In some cases, however, the yield surface and initial stress state are such that a significant part of the initial stress-strain response will be purely elastic. In such cases,
and
can be estimated as shown in Figure 11.10. That is, the initial elastic part of the stress-strain curve (up to a level of
) is ignored and
is taken as the axial strain at the halfway point to failure with respect to the remaining elastoplastic part of the stress-strain curve.
 |
12 HOEK-BROWN
The Hoek-Brown criterion is commonly used to describe the strength of fractured rock. The Hoek-Brown model implemented in OPTUM G2 uses the 2007 version of the Hoek-Brown criterion [HoekBook:2007]Author: E.~Hoek
Note: Available at: http://www.rocscience.com
Title: Practical Rock Engineering
Year: 2007 as the failure criterion while the Mohr-Coulomb surface is used as the plastic potential. In addition, it is possible to incorporate a compression cap as in the Mohr-Coulomb model. Similarly, regarding elasticity, the simple linear elastic model is used.
as the failure criterion while the Mohr-Coulomb surface is used as the plastic potential. In addition, it is possible to incorporate a compression cap as in the Mohr-Coulomb model. Similarly, regarding elasticity, the simple linear elastic model is used.
Material, Drainage, Stiffness
See Section 8.
Strength
The Hoek-Brown yield function is given by:
with
where is the Geological Strength Index,
is the uniaxial compressive strength of the intact rock,
is a material constant, and
is the disturbance factor. In OPTUM G2, the following parameters are used as input:
- Geological Strength Index,
.
- Uniaxial compressive strength of the intact rock,
[kPa].
- Intact rock parameter,
.
- Disturbance factor,
.
Flow Rule
The Hoek-Brown model makes use of a Mohr-Coulomb flow potential (see Section 8) with a variable dilation angle. For pure tension, the dilation angle is corresponding to separation. The dilation angle then decreases with
to a user specified value of
for
. A further linear decrease then takes place until
, where
is a user defined parameter, after which the dilation angle remains at zero. In summary, the dilation angle varies with
according to (see also Figure 12.1):
 |
As with the Mohr-Coulomb and Drucker-Prager models, it is also possible to use an associated flow rule in which case the plastic potential is the Hoek-Brown yield function. The parameters and settings of the Flow Rule category are:
- Flow Rule (Associated/Nonassocited)
- Flow Rule = Nonassociated: Dilation angle
[
]
- Flow Rule = Nonassociated: Dilation Cap (Yes/No) – Dilation Cap = Yes:
[kPa]
- Flow Rule = Nonassociated: Dilation angle
Compression cap, Unit Weights, Initial Stresses, Permeability
See Section 8.
12.1 Strength
Guidelines for estimating the four Hoek-Brown parameters ,
,
and
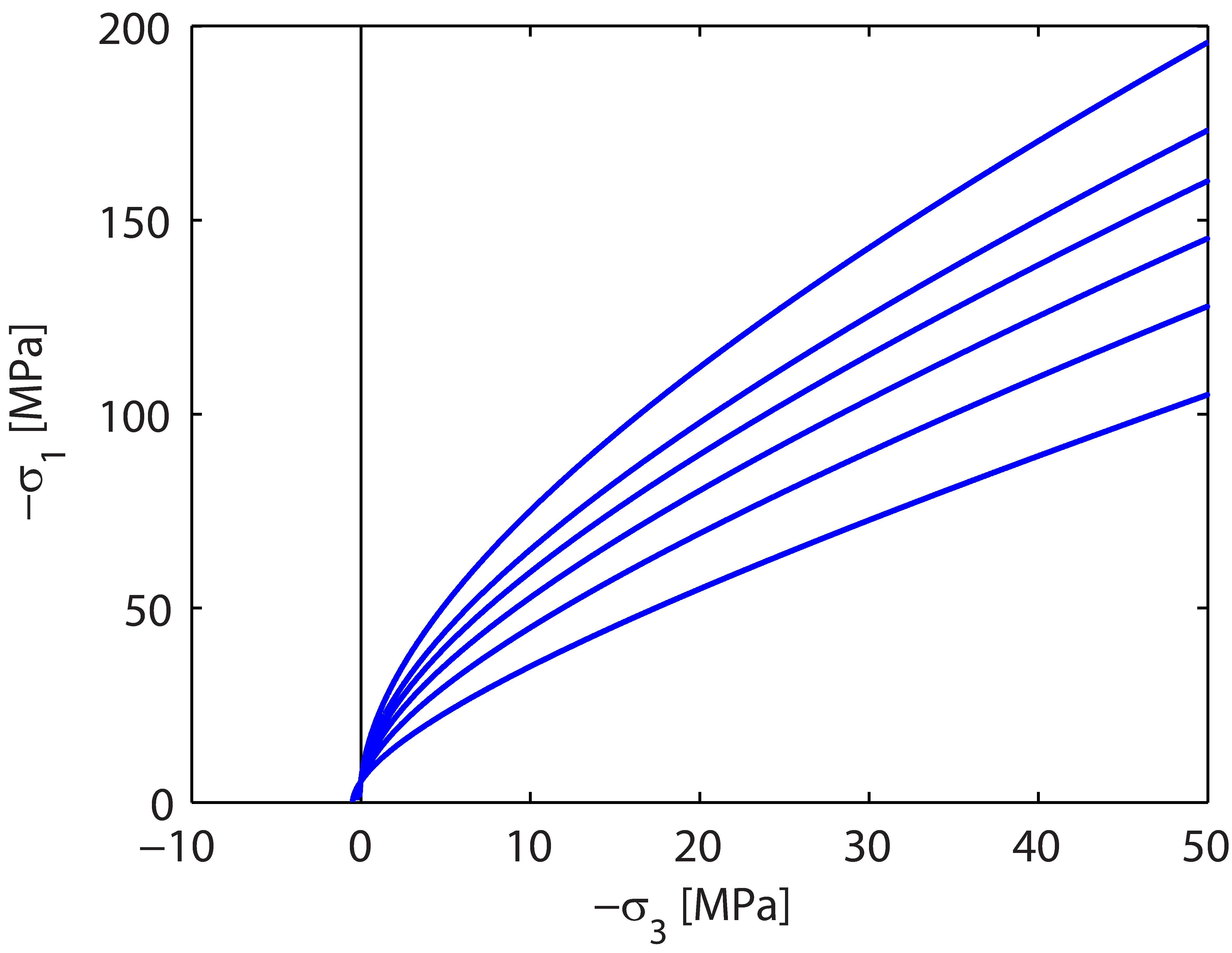
are provided in Figures 12.4-12.8. Some typical Hoek-Brown yield envelopes are shown in the Figures below.
 |
 |
 |
 |
 |
 |
 |
12.2 Elastic parameters
There are several empirical equations relating the elastic parameters to measures of rock type and quality. For Young’s modulus, [HoekBook:2007]Author: E.~Hoek
Note: Available at: http://www.rocscience.com
Title: Practical Rock Engineering
Year: 2007 quotes the following correlation:
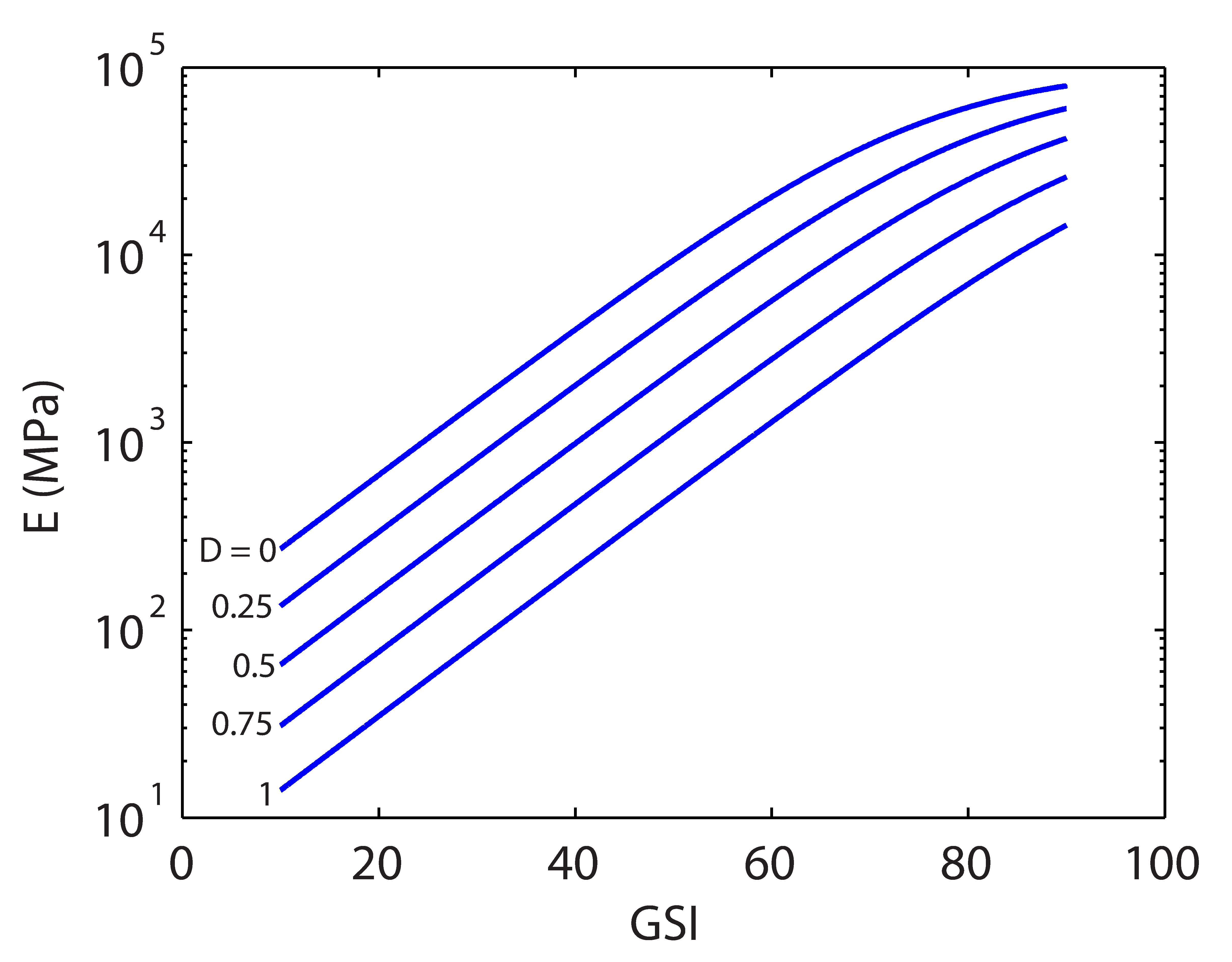
quotes the following correlation:
The variation of with
for different values of
is shown in Figure 12.9.
 |
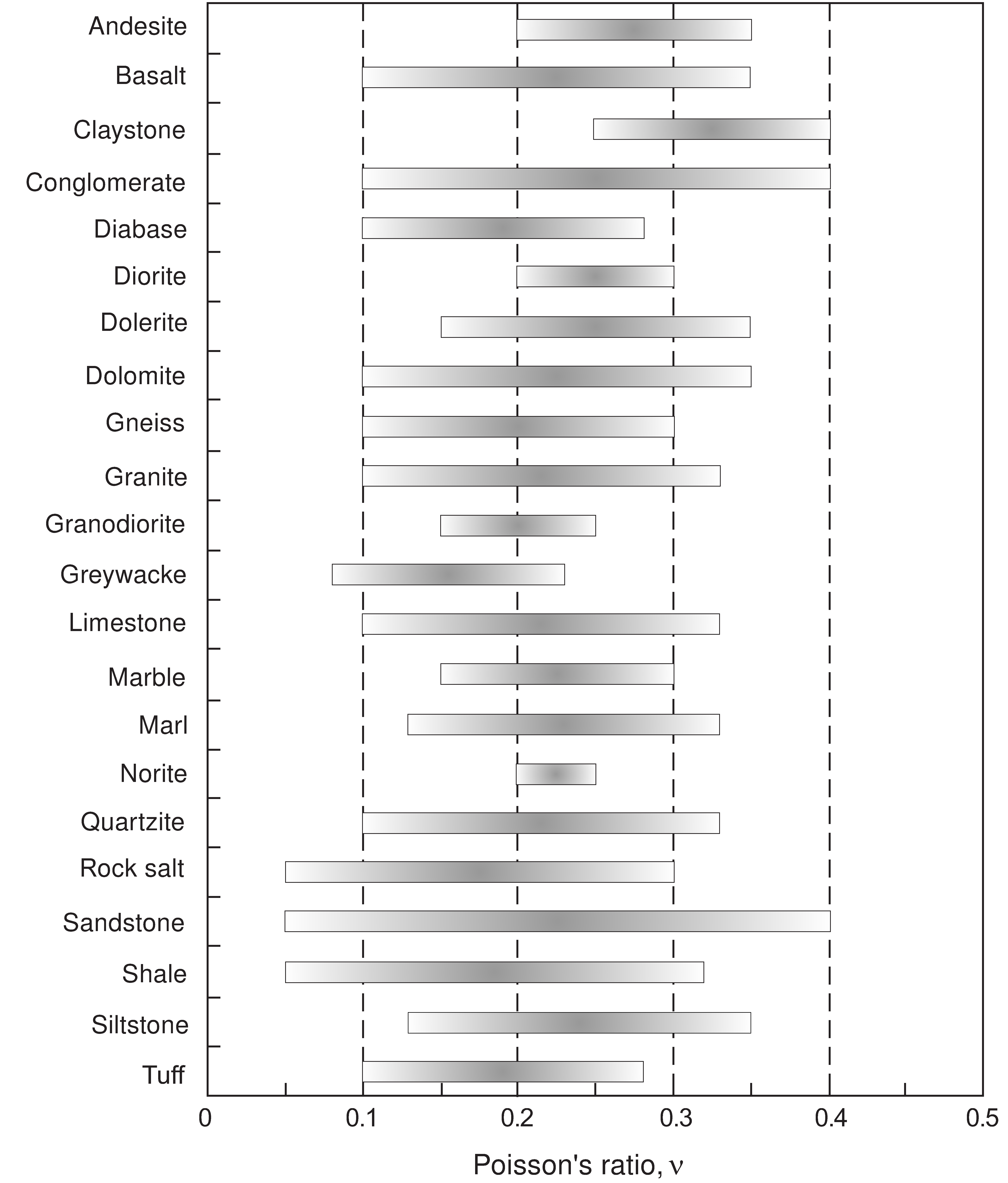
For most rock types Poisson’s ratio falls in the range of to
, with a significant variation within the same rock type (see Figure 12.10).
 |
12.3 Relation to Mohr-Coulomb parameters
Following the approach described by [HoekBook:2007]Author: E.~Hoek
Note: Available at: http://www.rocscience.com
Title: Practical Rock Engineering
Year: 2007 , the curved Hoek-Brown yield envelope may be approximated by the Mohr-Coulomb model using the standard Mohr-Coulomb cone augmented with a tension-cutoff.
, the curved Hoek-Brown yield envelope may be approximated by the Mohr-Coulomb model using the standard Mohr-Coulomb cone augmented with a tension-cutoff.
Firstly, with reference to the Mohr-Coulomb model implemented in OPTUM G2, the tension cut-off parameters are given by
[kPa]
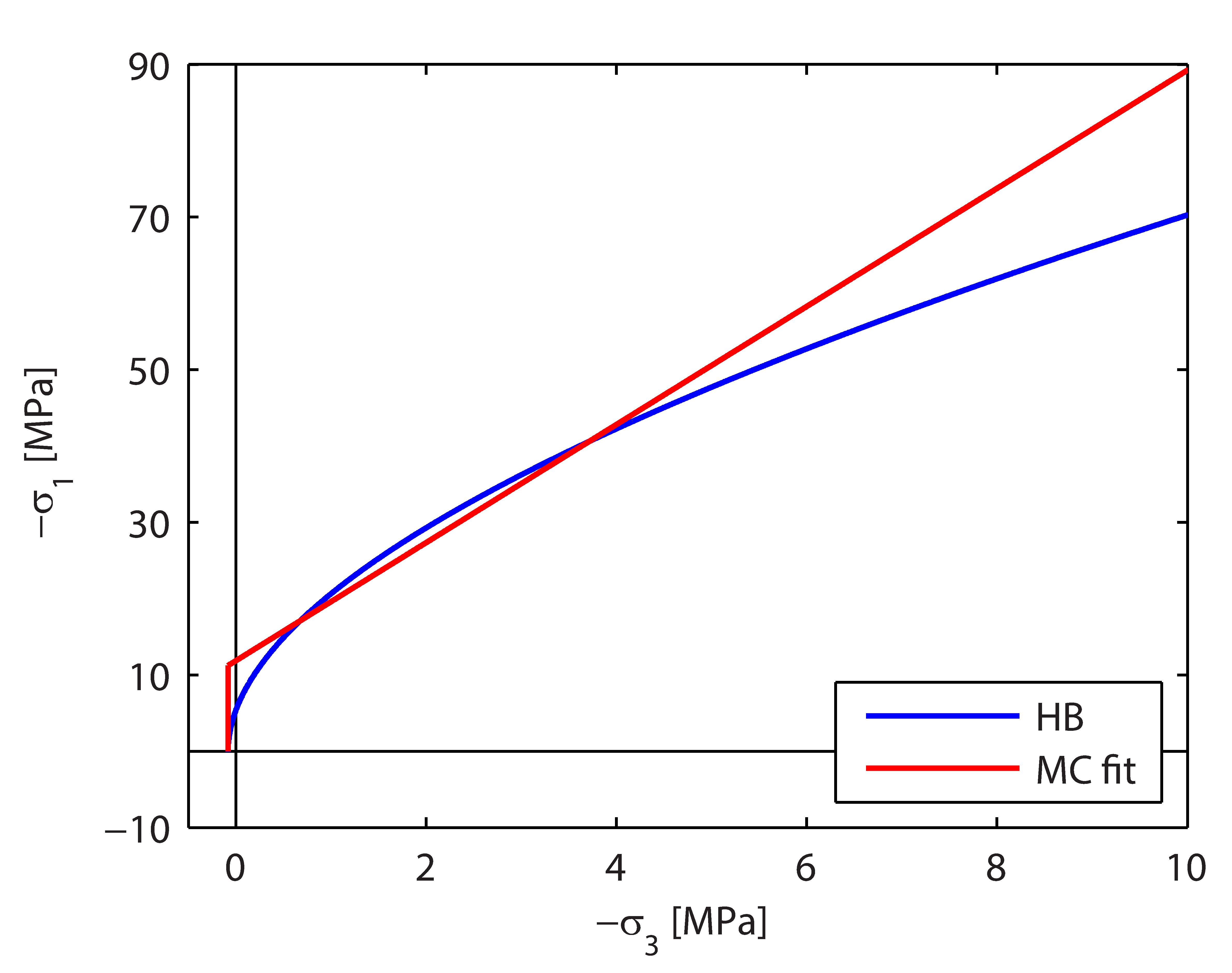
Secondly, a best-fit Mohr-Coulomb line in the interval between , leads to the following Mohr-Coulomb parameters:
[kPa]
where with
being positive in compression. An example of a fit is shown in Figure 12.11.
 |
As a rule of thumb, [HoekBook:2007]Author: E.~Hoek
Note: Available at: http://www.rocscience.com
Title: Practical Rock Engineering
Year: 2007 suggests that a first estimate of
suggests that a first estimate of may be taken as
.
12.4 Strength reduction
In Strength Reduction analysis (see the Analysis Manual), the Hoek-Brown criterion is treated by reducing the parameters and
equally to induce a state of collapse. The resulting factor is the strength based factor of safety:
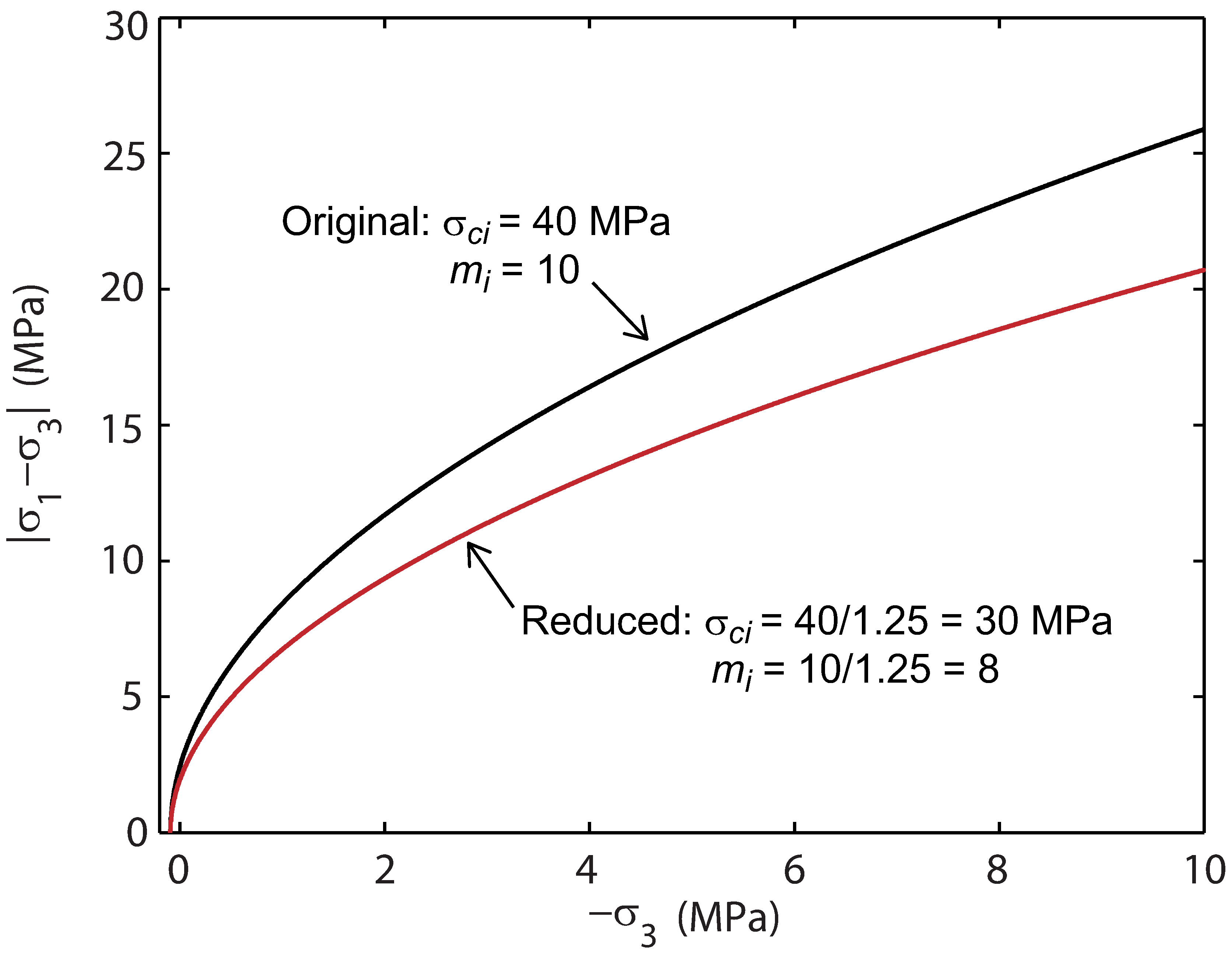
An example of the difference between the original yield envelope and that resulting from a factor of 1.25 is shown in Figure 12.12. While the decision as to which parameters are reduced is quite subjective, the approach used for the Hoek-Brown criterion is consistent with the one used for the Mohr-Coulomb criterion. As such, the tensile strength is unaffected by the reduction.
 |
13 GSK
The GSK model is similar to the Hoek-Brown model in that a curved yield surface is used in place of the Mohr-Coulomb yield surface. The GSK yield function is a generalization of the one proposed by [SK:2012]Author: S.~Krabbenhoft; J.~Clausen; L.~Damkilde
Journal: Advances in Civil Engineering
Pages: 1--10
Title: The Bearing Capacity of Circular Footings in Sand: Comparison betweenModel Tests and Numerical Simulations Based on a Nonlinear {M}ohr Failure Envelope
Volume: Article ID: 947276
Year: 2012 to account for the pressure dependence of the peak strength of granular materials such as sands, particularly at low stress levels. The generalized model allows for including a finite tensile strength. An attractive feature of the GSK criterion is that all parameters involved (four in total) may be interpreted in terms of the standard Mohr-Coulomb criterion.
to account for the pressure dependence of the peak strength of granular materials such as sands, particularly at low stress levels. The generalized model allows for including a finite tensile strength. An attractive feature of the GSK criterion is that all parameters involved (four in total) may be interpreted in terms of the standard Mohr-Coulomb criterion.
Strength
The strength parameters may be specified in terms of two parameter sets: General and NGI Sand.
13.1 Parameter Set General
The yield function is given by:
where
with the input parameters being:
- Friction angle at low stress levels,
[
].
- Friction angle at high stress levels,
[
].
- Apparent cohesion at high stress levels,
[kPa].
- Tensile strength,
[kPa].
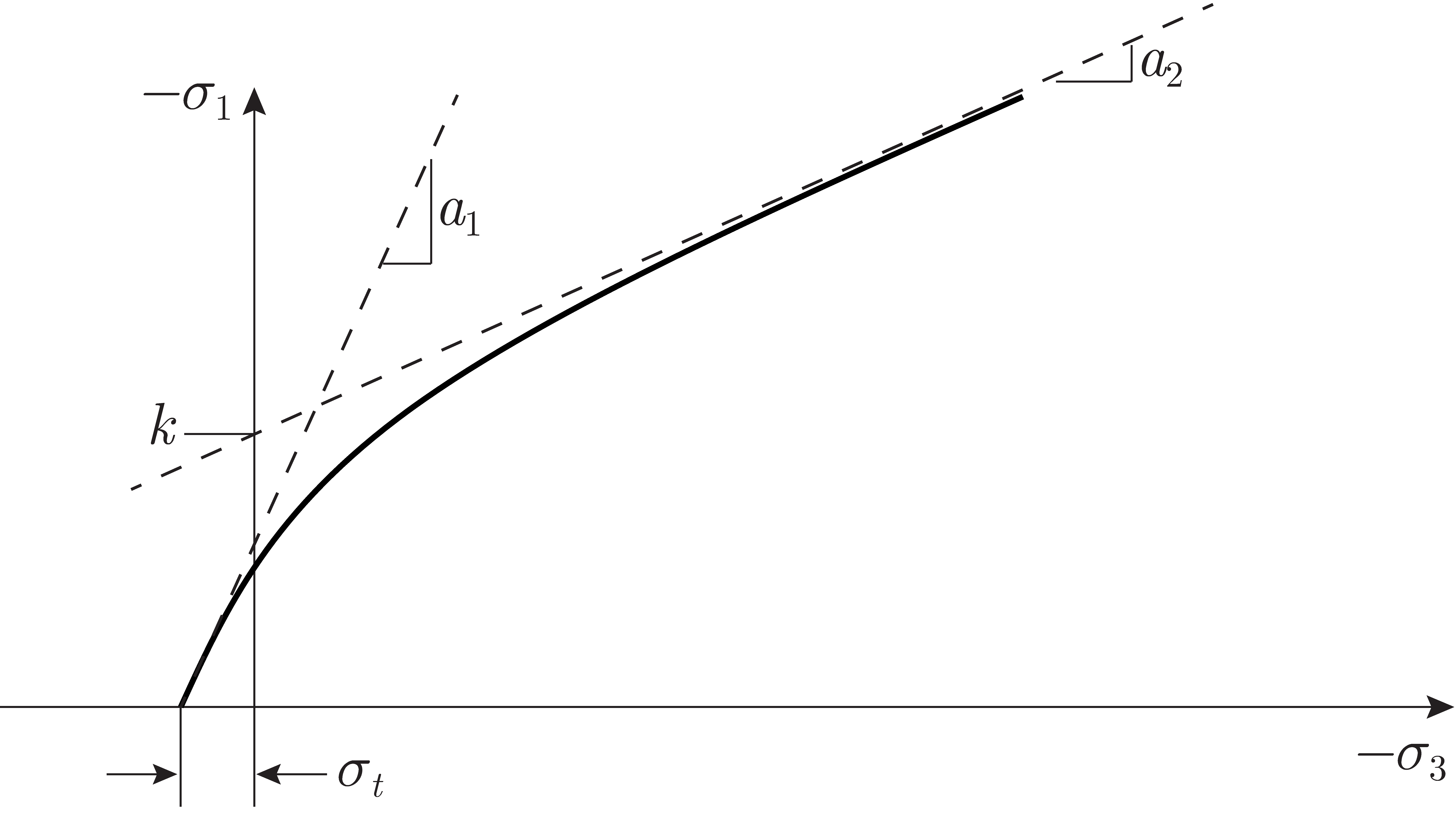 |
The GSK yield envelope is shown in Figure 13.1. It may be interpreted as a nonlinear Mohr-Coulomb envelope with friction angle and cohesion
given by (see Figure 13.2):
where
 |
For cohesionless materials such as sands, the strength is often specified in terms of the secant friction angle, , defined by
where is the stress ratio at failure (see Figure 13.3). For the GSK model, the secant friction angle is given by
where is given by Eq.13.4. With the secant friction angle at three different stress states, the three GSK parameters,
,
and
(or, equivalently,
,
and
) can be determined.
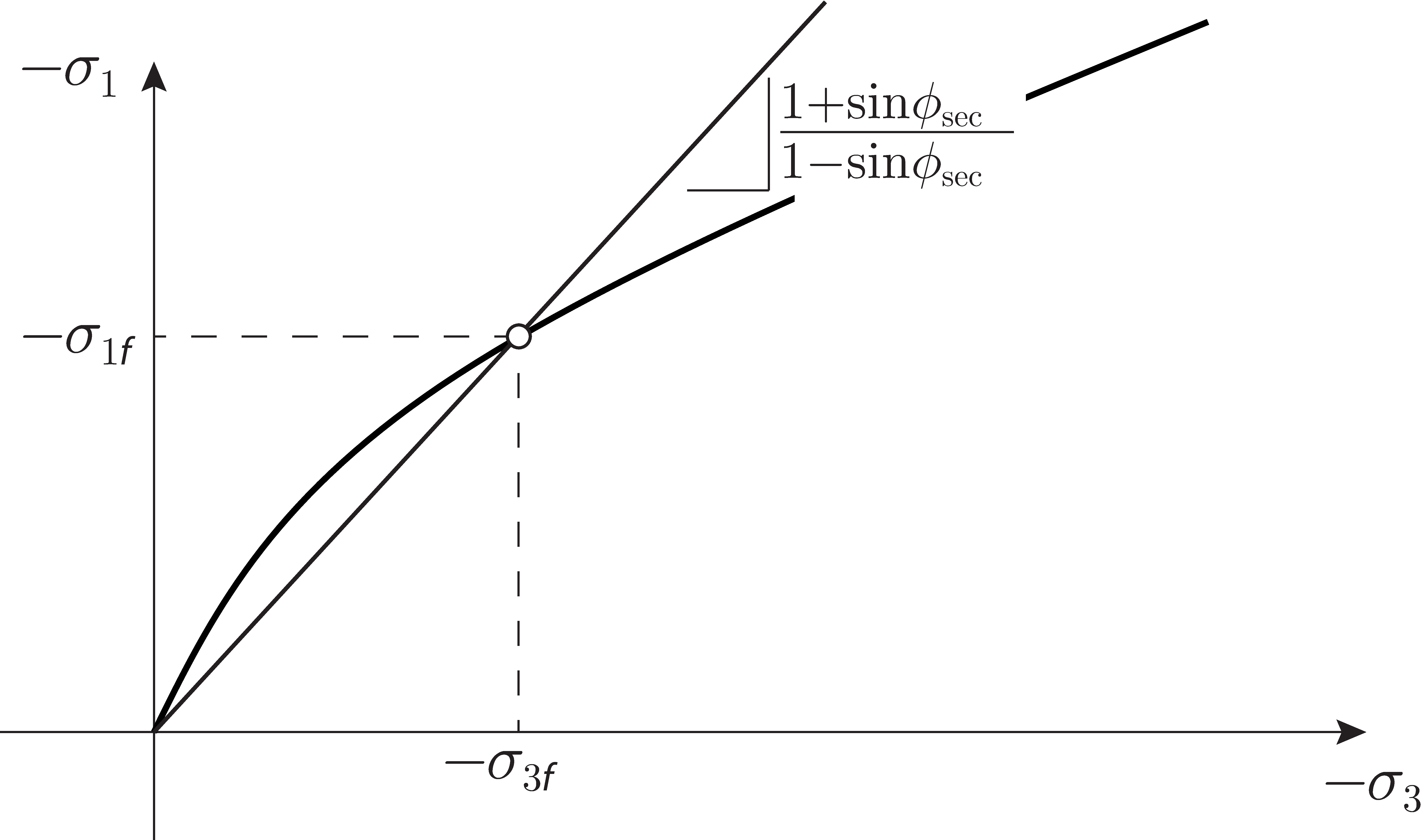 |
13.2 Parameter Set NGI Sand
This parameter set is a specialization of the general model to sands. The input parameters are:
- Relative density,
.
- Deviatoric Fit (Triaxial Compression/Plane Strain).
- Davis Correction (Yes/No).
On the basis of the relative density, the GSK parameters ,
and
(
is always zero), have been fitted to a collection of triaxial data compiled at the Norwegian Geotechnical Institute [Andersen:2013]Author: K.~H.~Andersen; K.~Schjetne
Journal: Journal of Geotechnical and Geoenvironmental Engineering
Pages: 1140-1155
Title: Database of Friction Angles of Sand and Consolidation Characteristics of Sand, Silt, and Clay
Volume: 139
Year: 2013 . The database covers a total of 54 different sands from 38 different sites of which 40-50% are offshore. The mean particle size of the sands is 0.23 mm and the average coefficient of uniformity is
. The database covers a total of 54 different sands from 38 different sites of which 40-50% are offshore. The mean particle size of the sands is 0.23 mm and the average coefficient of uniformity is . The average friction angles reported by [Andersen:2013]Author: K.~H.~Andersen; K.~Schjetne
Journal: Journal of Geotechnical and Geoenvironmental Engineering
Pages: 1140-1155
Title: Database of Friction Angles of Sand and Consolidation Characteristics of Sand, Silt, and Clay
Volume: 139
Year: 2013 can be fitted by the GSK model using:
can be fitted by the GSK model using:
These parameters are used for the settings Deviatoric Fit Triaxial Compression and Davis Correction
No. The parameters are shown in Figure 13.5.
For Deviatoric Fit Plane Strain and Davis Correction
No, the triaxial parameters are modified on the basis of the relation proposed by [Stakemann:1976]Author: O.~Stakemann
Institution: Internal Memo I.M. 1976-1, Danish Geotechnical Institute
Note: In Danish
Title: Brudbetingelse for {G12}-sand og plane modelfors�g ({F}ailure conditions for {G12}-sand and plane strain model tests)
Year: 1976 :
:
Finally, to take the effects of nonassociativity into account in an approximate manner when conducting Limit Analysis and Strength Reduction, the reduced angles proposed by [Davis:1968]Address: Butterworth, London
Author: E.~H.~Davis
Booktitle: Soil Mechanics: Selected Topics
Editor: I.~K.~Lee
Pages: 341--380
Title: Theories of plasticity and the failure of soil masses
Year: 1968 are used for setting Davis Correction
are used for setting Davis Correction Yes. Assuming a dilation angle given by
, the above parameters are reduced as:
and
 |
It should be noted that the Davis correction applies only to Limit Analysis and Strength Reduction. For all other analysis, no correction is applied.
The four sets of friction angles, computed by Eq.13.6, are shown in Figure 13.4 as function of for selected
. [Andersen:2013]Author: K.~H.~Andersen; K.~Schjetne
Journal: Journal of Geotechnical and Geoenvironmental Engineering
Pages: 1140-1155
Title: Database of Friction Angles of Sand and Consolidation Characteristics of Sand, Silt, and Clay
Volume: 139
Year: 2013 present their data as friction angle versus relative density for a selection of intervals of the octahedral consolidation stress. These data have been converted to the present form by converting the mean value of the octahedral consolidation stress in each interval into
present their data as friction angle versus relative density for a selection of intervals of the octahedral consolidation stress. These data have been converted to the present form by converting the mean value of the octahedral consolidation stress in each interval into assuming an earth pressure coefficient of
.
 |
Flow Rule
The GSK model offers three different possibilities for specifying the flow rule:
- Associated. Standard associated flow rule the flow potential equal to the GSK yield function.
- GSK. Nonassociated flow rule with a dilation angle
where
is the current equivalent Mohr-Coulomb friction angle and
is a parameter. This is similar to the flow rule of the Bolton model (see Section 14).
- Constant Dilation. Nonassociated flow rule with a constant dilation angle equal to
except for
where it varies linearly between
and
as shown in Figure 13.6.
The GSK and Constant Dilation flow rules may be further augmented by a strain based dilation cap as in the Mohr-Coulomb model.
 |
Compression Cap, Unit Weights, Initial Stresses, Permeability
See Section 8.
13.3 Application to rock
While the Hoek-Brown model is available for the modeling of fractured rock masses, the GSK model is in many cases capable of reproducing typical experimental data rather well. Two examples are shown in Figure 13.8 where triaxial test data for a limestone and a sandstone have been fitted by the GSK criterion.
13.4 Strength reduction
In Strength Reduction analysis (see the Analysis Manual), the GSK criterion is treated by reducing the parameters ,
and
equally (see Figure 13.9) to induce a state of collapse. The resulting factor is the strength based factor of safety:
While the decision as to which parameters are reduced is quite subjective, the approach used for the GSK criterion is consistent with the one used for the Mohr-Coulomb criterion. As such, the tensile strength is unaffected by the reduction.
 |
13.5 Notes
The GSK criterion is convex only for
Analyses with parameter sets not satisfying this inequality will not be processed.
14 BOLTON
The Bolton model incorporates the stress-dilatancy correlations for sands proposed by [Bolton:1986]Author: M.~D.~Bolton
Journal: Geotechnique
Pages: 65--78
Title: The strength and dilancy of sands
Volume: 36
Year: 1986 . These correlations provide peak friction and dilation angles as function of stress level and relative density. For a fixed density, the resulting failure envelope is nonlinear and similar to those of Hoek-Brown and GSK, i.e. the apparent friction angle increases with decreasing mean stress.
. These correlations provide peak friction and dilation angles as function of stress level and relative density. For a fixed density, the resulting failure envelope is nonlinear and similar to those of Hoek-Brown and GSK, i.e. the apparent friction angle increases with decreasing mean stress.
Material, Drainage, Stiffness
See Section 8.
Strength
The yield function of the Bolton model is of the Mohr-Coulomb type with a pressure and density dependent friction angle:
The friction angle is given by
where is the constant-volume (critical-state) friction angle,
is a model parameter and
is the relative dilatancy. The latter quantity is defined by [Bolton:1986]Author: M.~D.~Bolton
Journal: Geotechnique
Pages: 65--78
Title: The strength and dilancy of sands
Volume: 36
Year: 1986 as:
as:
where is the relative density,
is the mean stress, and
and
and model parameters. [Bolton:1986]Author: M.~D.~Bolton
Journal: Geotechnique
Pages: 65--78
Title: The strength and dilancy of sands
Volume: 36
Year: 1986 suggests that
suggests that is limited by:
While some evidence for very large friction angles at very low stresses levels is available [e.g [Alshibli:2003]Author: K.~A.~Alshibli; S.~N.~Batiste; S.~Sture
Journal: Journal of Geotechnical and Geoenvironmental Engineering
Pages: 483--494
Title: Strain Localization in Sand: Plane Strain versus Triaxial Compression
Volume: 129
Year: 2003 ] implements the above limits.
] implements the above limits.
In summary, the Bolton model requires specification of five parameters:
- The constant-volume (critical-state) friction angle
. Typical values are in the range of
with
often being reported [Bolton:1986]Author: M.~D.~Bolton
Journal: Geotechnique
Pages: 65--78
Title: The strength and dilancy of sands
Volume: 36
Year: 1986 .
. - The relative density
varying between 0 and 1.
- The model parameter
. [Bolton:1986]Author: M.~D.~Bolton
Journal: Geotechnique
Pages: 65--78
Title: The strength and dilancy of sands
Volume: 36
Year: 1986 links this to the particle crushing strength,
links this to the particle crushing strength, , by
and suggests values of
for quartz and feldspar grains down to
for limestone,
for anthracite, and
for chalk.
- The model parameter
. [Bolton:1986]Author: M.~D.~Bolton
Journal: Geotechnique
Pages: 65--78
Title: The strength and dilancy of sands
Volume: 36
Year: 1986 suggests a value of
suggests a value of for a wide range of sands.
- The model parameter
. [Bolton:1986]Author: M.~D.~Bolton
Journal: Geotechnique
Pages: 65--78
Title: The strength and dilancy of sands
Volume: 36
Year: 1986 suggests values of
suggests values of for triaxial compression and
for plane strain. However, significantly lower values have also been reported, e.g.
by [White:2008]Author: D.~J.~White; K.~L.~Teh; C.~F.~Leung; Y.~K.~Chow
Journal: Geotechnique
Pages: 781--792
Title: A comparison of the bearing capacity of flat and conical circular foundations on sand
Volume: 58
Year: 2008 .
.
The variation of the friction angle with mean stress is shown in Figure 14.1 for some typical parameter sets.
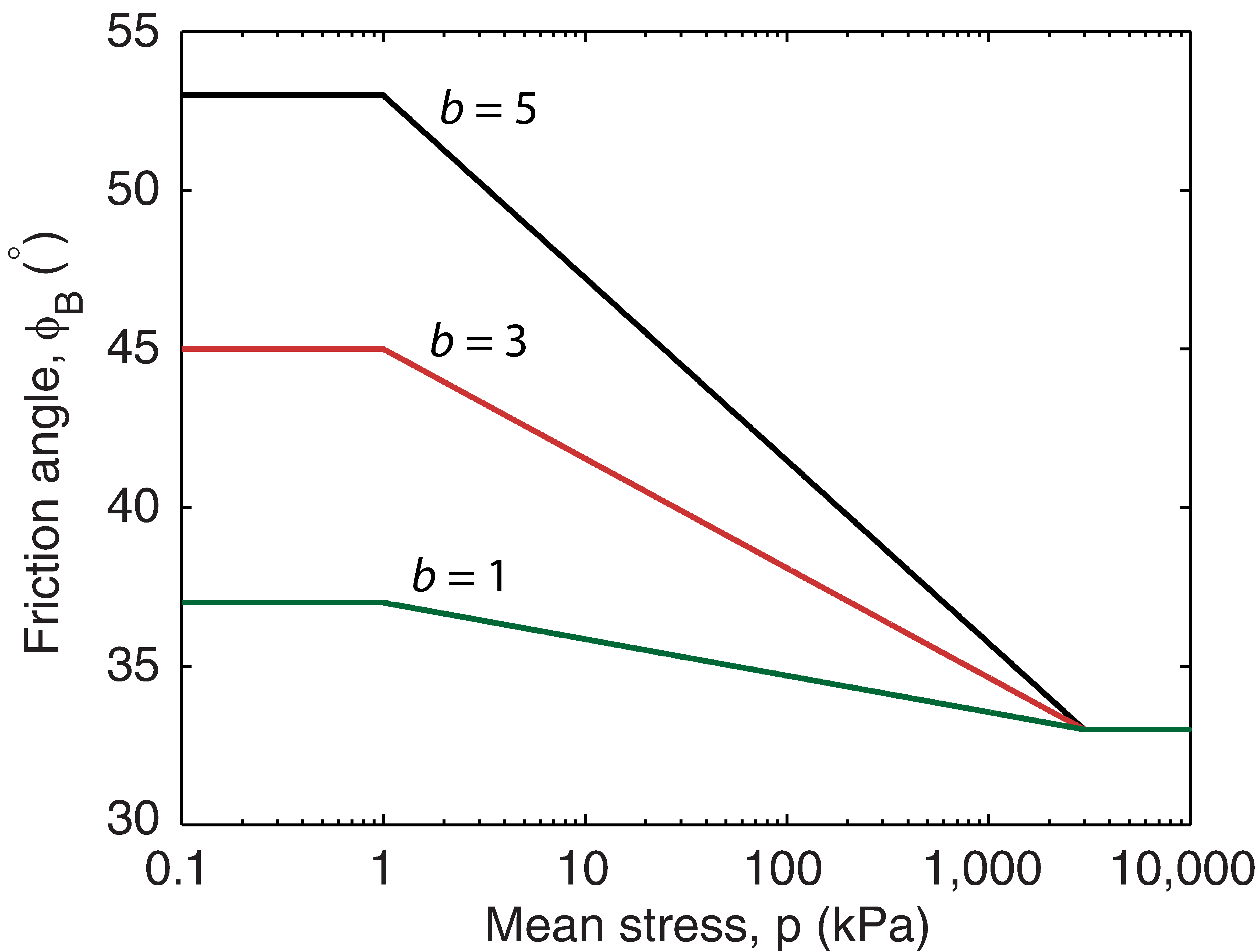 |
Flow Rule
The flow potential of the Bolton model is given by
The Bolton model provides a choice of two flow rules:
- Associated. Standard associated flow rule with
.
- Bolton. Nonassociated flow rule with
where
is a parameter. The original relations published by Bolton recommended
.
In both cases, the dilation can be limited by a Dilation Cap of the Mohr-Coulomb type (see Section 8).
Compression Cap, Unit Weights, Initial Conditions, Hydraulic Model
See Section 8.
14.1 Strength reduction
In Strength Reduction analysis (see the Analysis Manual), the Bolton criterion is treated by reducing the friction angle to induce a state of collapse. The resulting factor is the strength based factor of safety:
While the decision as to which parameters are reduced is quite subjective, the approach used for the Bolton criterion is consistent with the one used for the Mohr-Coulomb criterion.
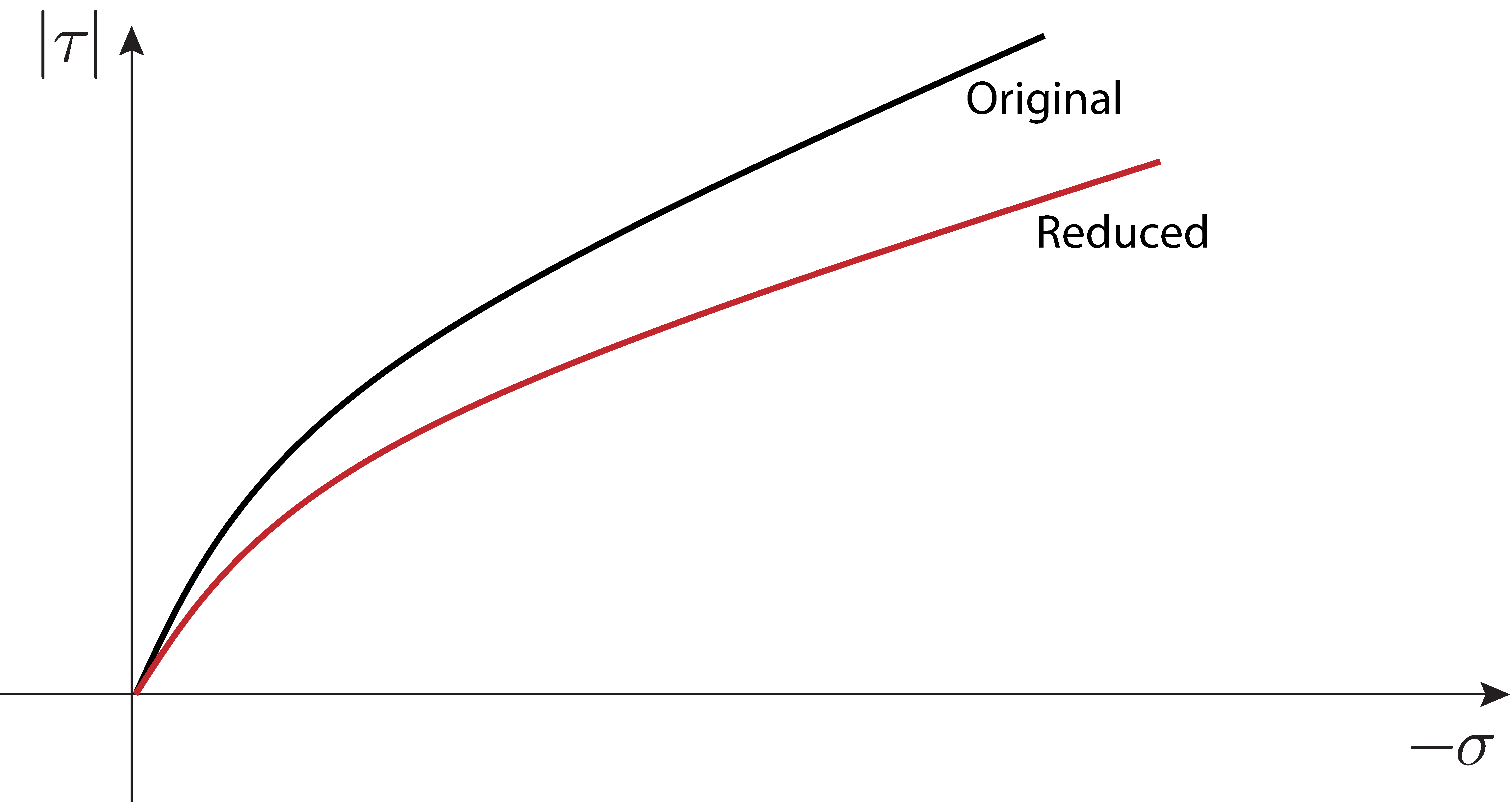 |
15 MODIFIED CAM CLAY
The critical state models developed by Roscoe and his coworkers [Roscoe:1968]Author: K.~H.~Roscoe; J.~B.~Burland
Booktitle: Engineering Plasticity
Editor: J.~Heyman and F.~A.~Leckie
Pages: 535--609
Publisher: Cambridge University Press
Title: On the generalized stress-strain behaviour of wet clay
Year: 1968 , [Schofield:1968]Author: A.~Schofield; P.~Wroth
, [Schofield:1968]Author: A.~Schofield; P.~Wroth
Note: Available online: http://www.geotechnique.info/
Publisher: Cambridge University Press
Title: Critical State Soil Mechanics
Year: 1968 in the 1960s have been widely applied in geomechanics and form the basis of a large number of later models. The Modified Cam Clay model of [Roscoe:1968]Author: K.~H.~Roscoe; J.~B.~Burland
in the 1960s have been widely applied in geomechanics and form the basis of a large number of later models. The Modified Cam Clay model of [Roscoe:1968]Author: K.~H.~Roscoe; J.~B.~Burland
Booktitle: Engineering Plasticity
Editor: J.~Heyman and F.~A.~Leckie
Pages: 535--609
Publisher: Cambridge University Press
Title: On the generalized stress-strain behaviour of wet clay
Year: 1968 has been particularly popular. A slightly extended version of this model (including a finite cohesion) is implemented in OPTUM G2 following the scheme proposed by [Krabbenhoft:2012CMAME]Author: K.~Krabbenhoft; A.~V.~Lyamin
has been particularly popular. A slightly extended version of this model (including a finite cohesion) is implemented in OPTUM G2 following the scheme proposed by [Krabbenhoft:2012CMAME]Author: K.~Krabbenhoft; A.~V.~Lyamin
Journal: Computer Methods in Applied Mechanics and Engineering
Pages: 239--249
Title: Computational {C}am clay plasticity using second-order cone programming
Volume: 209--212
Year: 2012 .
.
The material parameters of Modified Cam Clay are to some extent interrelated and it is not possible to distinguish as sharply between strength and stiffness parameters as for other materials. In the following, the parameters are described in the sequence that they appear in OPTUM G2.
Stiffness
One of the basic premises of Modified Cam Clay is that the specific volume versus effective mean stress in isotropic compression may be described by a relation of the type shown in Figure 15.1. In terms of elastoplasticity theory, the normal compression line may be interpreted as an elastoplastic branch while the response on an unloading/reloading line is elastic.
 |
With reference to Figure 15.1, the response in elastoplastic loading is given by
while, the governing equation for unloading/reloading is
In conventional oedometer tests where the void ratio is plotted as function of the base 10 logarithm of the vertical stress (see Figure 15.1). It may be shown that the Modified Cam Clay parameters and
are related to the conventional oedometric parameters,
and
, by
While the relation between and
is not exact it is usually a good approximation [see [Wood:1990]Author: D.~{Muir~Wood}
Publisher: Cambridge University Press
Title: Soil Behaviour and Critical State Soil Mechanics
Year: 1990 for details].
for details].
For Modified Cam Clay, the incremental stress-strain relation may be written as
where is the recompression index,
is the compression index, and
is the void ratio which is related to the volumetric strain by
where is the initial void ratio and
is the volumetric strain (positive in compaction).
From the elastic part of Eq.15.4, a tangent bulk modulus can be identified as
By introducing a Poisson’s ratio, a tangent shear modulus is introduced as:
Together, and
define a tangent elastic modulus,
such that the general three-dimensional elastic stress-strain relation is given by
In summary, the three stiffness parameters are:
- Recompression index,
- Compression index,
- Poisson’s ratio,
The initial void ratio, , is considered part of the initial conditions (see below).
Strength
The conventional Modified Cam Clay model makes use of a hardening yield surface given by
where
with being the preconsolidation pressure which acts as a hardening variable. The friction parameter
is related to the frictional angle by
where
is the Lode angle.
In OPTUM G2, cohesion is introduced by defining a new pressure variable:
where is the cohesion. The yield surface is then given by:
For fixed , the yield functions
define ellipses in
-
space with the critical state line,
, passing through the top point (see Figure 15.2).
 |
The yield surface hardens or softens according to the following relation between and the volumetric plastic strain:
where is the compression index and the plastic strains follow from the associated flow rule:
Thus, for plastic compaction () the yield surface expands (hardens) while plastic dilation (
) leads to a shrinking (softening) of the yield surface. At the critical state,
, the plastic volumetric strain rate is zero and the yield surface undergoes no further changes (see Figure 15.2).
Finally, while the critical state line in the basic Modified Cam Clay model is approached asymptotically by virtue of the hardening rule, the model implemented in OPTUM G2 gives the possibility to include as an explicit constraint. In this way, the critical state line cannot be crossed and the softening that would otherwise take place is prevented. This additional constraint may be included via the CSL Constraint field.
In summary, the strength parameters of Cam clay are:
- Cohesion,
[kPa]
- Friction angle,
- CSL Constraint (Yes/No)
Setting CSL Constraint = Yes invokes the additional constraint (see Figure 15.3). The CSL constraint is useful both numerically, as it eliminates potential softening, and physically, as it limits the possibly excessive strength implied by high overconsolidation ratios. The plastic volumetric strains associated with the CSL constraint are always zero, i.e. the flow rule of CSL the constraint is nonassociated with a dilation angle of zero.
 |
Initial Conditions
As for all other materials, the initial stresses can be generated by an Initial Stress analysis (manually or as part of other analyses). This requires specification of the earth pressure coefficient and is done such that the resulting stress state is limited by the critical state line, i.e. the CSL constraint is effectively imposed.
With a set of initial stresses at hand, the initial value of needs to be specified. This is done in terms of the overconsolidation ratio:
where and
are the initial preconsolidation pressure and effective mean stress respectively. The above overconsolidation ratio differs from the usual overconsolidation ratio defined by
where is the vertical preconsolidation stress and
is the initial vertical effective stress (corrected for a possible cohesion). The two different overconsolidation ratios are related by
where is earth the pressure coefficient for the soil in its initial normally consolidated state and
is the earth pressure coefficient for the soil in its current, possibly overconsolidated, state. It is common practice to relate these coefficients to the friction angle and the overconsolidation ratio by
In OPTUM G2, the earth pressure coefficient taken as input is the current earth pressure coefficient, i.e. , while the earth pressure coefficient corresponding to normally consolidated conditions is calculated automatically from Eq.15.20.
In summary, the parameters related to the initial state are:
- Initial void ratio,
- Overconsolidation ratio, OCR
- Earth pressure coefficient,
Regarding the calculation of the following should be noted. As a general rule, we have
where
is the initial effective pressure. However, depending on the initial value of the deviatoric stress
, the yield condition may not be satisfied for
(see Figure 15.4). To counter this situation and satisfy the yield condition
,
is adjusted to the smallest value,
, that will ensure
. This means that the actual
(and thereby OCR) under which the calculations are initiated may be slightly higher than that specified.
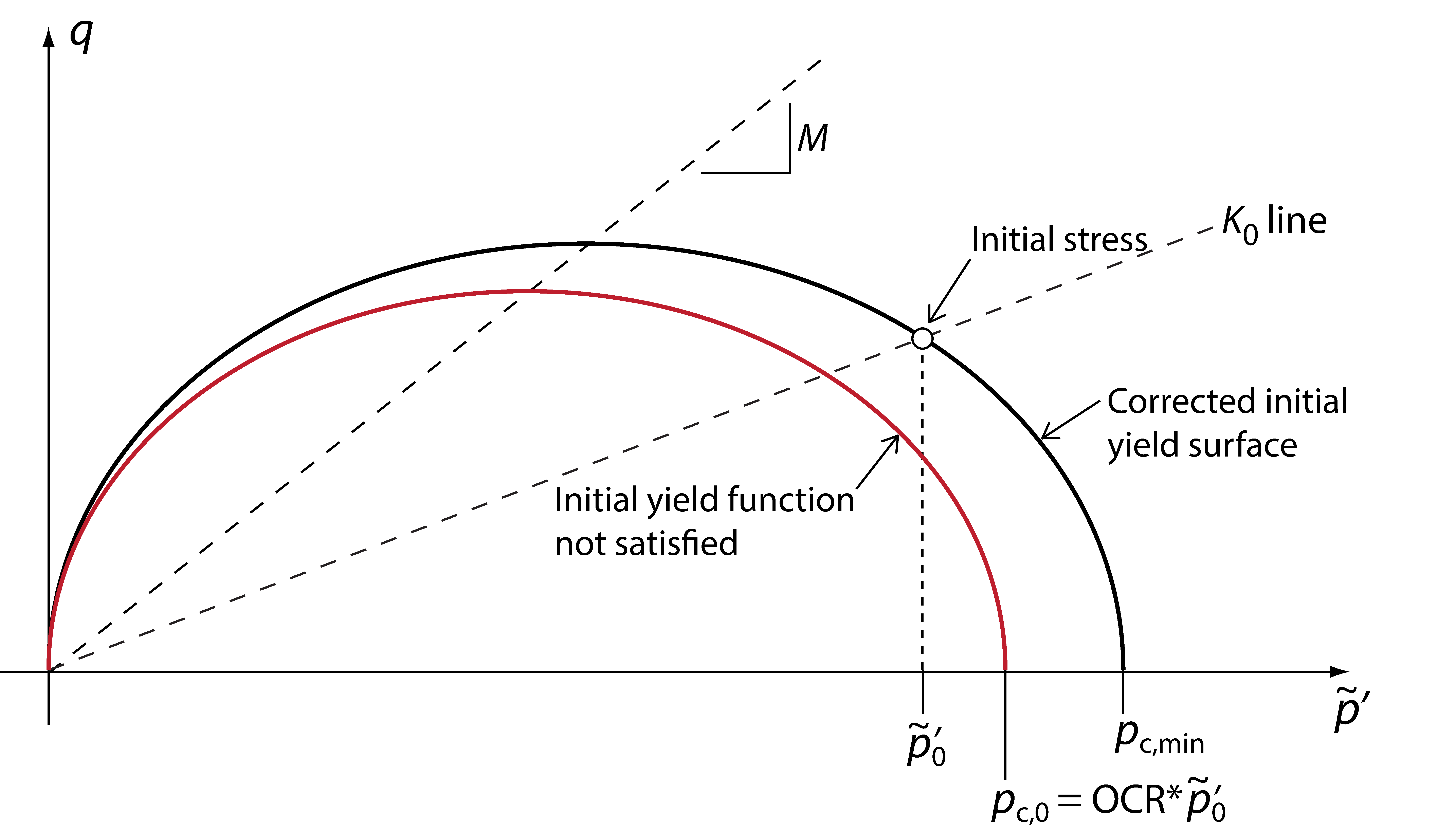 |
Unit Weights, Hydraulic Model
See Section 8.
15.1 Limit Analysis and Strength Reduction
For the Modified Cam Clay model, Limit Analysis and Strength Reduction are conducted by calculating equivalent Tresca (Standard or Generw parameters and then proceeding as for these materials.
15.1.1 Drained conditions
Under drained conditions, the strength is governed by the material parameter . Due to the effect of nonassociativity (the dilation is zero at the critical state) it may be shown that a limit analysis equivalent to a full elastoplastic analysis should be conducted at a slightly lower value of
[see [Krabbenhoft:2012IJNME]Author: K.~Krabbenhoft; M.~R.~Karim; A.~V.~Lyamin; S.~W.~Sloan
Journal: International Journal for Numerical Methods in Engineering
Pages: 1089--1117
Title: Associated computational plasticity schemes for nonassocited frictional materials
Volume: 89
Year: 2012 for details]. It should also be borne in mind that localization – accompanied by an apparent softening – is possible even for low to moderate overconsolidation ratios [Krabbenhoft:2012CMAME]Author: K.~Krabbenhoft; A.~V.~Lyamin
for details]. It should also be borne in mind that localization – accompanied by an apparent softening – is possible even for low to moderate overconsolidation ratios [Krabbenhoft:2012CMAME]Author: K.~Krabbenhoft; A.~V.~Lyamin
Journal: Computer Methods in Applied Mechanics and Engineering
Pages: 239--249
Title: Computational {C}am clay plasticity using second-order cone programming
Volume: 209--212
Year: 2012 . The ultimate limit loads found by means of Limit Analysis will therefore usually only be in approximate agreement with those found from a full elastoplastic analysis to failure.
. The ultimate limit loads found by means of Limit Analysis will therefore usually only be in approximate agreement with those found from a full elastoplastic analysis to failure.
15.1.2 Undrained conditions
Under undrained conditions, an equivalent undrained shear strength can be calculated and the Mohr-Coulomb or Tresca model then used to conduct the Limit Analysis. With the initial preconsolidation pressure and effective mean stress known, the equivalent undrained shear strength is given by
where is the earth pressure coefficient and
is the initial vertical effective stress which is assumed to be related to the horizontal stress by
.
From the above expression it will be seen that the undrained shear strength at the ground surface () is zero unless
is finite. In most cases, this is not reasonable and some finite amount of cohesion should therefore be used. Moreover, by varying
as well as OCR and
with depth, typical undrained shear strength profiles can in most cases be matched well. Some examples are shown in Figures 15.5 and 15.6. In these figures,
,
and
are varied with depth while the remaining parameters are kept fixed at:
,
,
, and
with
being the depth coordinate and
kN/m
the effective unit weight. The Lode angle as been set to
.
 |
 |
15.2 Creep
For certain clays, creep (or secondary compression) accounts for a significant part of the total deformation. An often used empirical law states that the volumetric creep strain following full primary consolidation is given by
where is the volumetric creep strain,
is the secondary compression coefficient,
is the void ratio,
is the time to 90% primary consolidation and
is the time at which the creep strain is evaluated. More generally, the increment in creep stain between two times
and
may be calculated as
The creep strain may be integrated to give the total settlement. For a layer of depth we have:
where is the increment of vertical settlement due to creep.
In OPTUM G2, creep is included using the approach of [Borja:1985]Author: R.~I.~Borja; E.~Kavazanjian
Journal: Geotechnique
Pages: 283--298
Title: A constitutive model for the stress-strain-time behaviour of `wet clays'
Volume: 35
Year: 1985 . The total strain is here given by
. The total strain is here given by
where and
are the usual elastic and plastic strains respectively and
is the creep strain. To describe the evolution of the creep strain with time, a creep potential,
, is introduced by
where is a material parameter (equivalent to
above),
is the void ratio and
is a constant which is set internally to
day. The evolution of the creep strain is then given by
where is a vector that gives the direction of the creep strain rate vector. Consistent with Modified Cam Clay, this quantity is taken as
where
In OPTUM G2, creep thus requires the specification of a single additional material parameter, . This parameter is specified as a fraction of
. The ratio
typically falls in the range of 0.02 to 0.1 for a wide variety of natural materials prone to creep [Mesri:1986]Author: G.~Mesri; A.~Castro
Journal: Journal of Geotechnical Engineering
Pages: 230--247
Title: ${C}_\alpha/{C}_c$ concept and ${K}_0$ during secondary compression
Volume: 113
Year: 1986 .
.
In the one-dimensional case, the above creep law leads to a volumetric creep strain given by
The increment in creep strain over a time increment from to
is thus given by
which, with , approaches the empirical relation Eq.15.23 for times significantly greater than
day.
16 HARDENING MOHR-COULOMB (HMC)
The Hardening Mohr-Coulomb (HMC) model is designed to remedy some of the shortcomings of the standard Mohr-Coulomb model described in Section 8. The HMC model was first proposed by [Wood:2004]Author: D.~{Muir Wood}
Publisher: Cambridge University Press
Title: Geotechnical Modelling
Year: 2004 with reference to triaxial stress space and later extended to general stress space by [Doherty:2013]Author: J.~P.~Doherty; D.~{Muir Wood}
with reference to triaxial stress space and later extended to general stress space by [Doherty:2013]Author: J.~P.~Doherty; D.~{Muir Wood}
Journal: Geotechnique
Pages: 661--673
Title: An extended {M}ohr-{C}oulomb ({EMC}) model for predicting the settlement of shallow foundations on sand
Volume: 63
Year: 2013 . The version of the model implemented in follows these developments closely while incorporating a number of new features that allow for a better match of the model to experimental data.
. The version of the model implemented in follows these developments closely while incorporating a number of new features that allow for a better match of the model to experimental data.
16.1 Typical soil behavior
The typical behaviour of soil in drained triaxial compression experiments is as sketched in Figure 16.1. Compared to metals and other non-granular materials, a distinguishing feature of soils is that the apparent stiffness in initial loading is significantly less than that observed when the sample is later unloaded and reloaded. To characterize the initial stiffness, use is often made of the secant modulus, , defined as:
where is the ultimate shear stress and
is the axial strain at half the ultimate shear stress. Similarly, in unloading/reloading, the stiffness is characterized by the modulus
. It should be noted that while
is an elastic stiffness in the usual sense, the physics leading to
comprise both elastic and plastic characteristics. In general, both
and
are pressure dependent and increase with increasing confining pressure. The ratio between the two moduli is usually in the range of
to 5 or higher.
 |
The ultimate shear stress is proportional to the pressure, , by
where
is a material parameter and
is the confining pressure at the ultimate limit state. In conventional triaxial compression where the stress path is such that
, the ultimate shear stress for a purely frictional material is given by
where is the confining pressure. Using the relation between
and the Mohr-Coulomb friction angle
in triaxial compression:
the ultimate shear stress is given by
In the general case, the relation between and
is given by
where
is the Lode angle (equal to in triaxial compression).
Regarding the strains, it is usually observed that the dilation which occurs at appreciable levels of shear strain is a function of the material density. Dense soils may undergo a significant amount of dilation under continued shearing while less dense soils will tend to dilate less or may even contract plastically, i.e. undergo negative dilation. These characteristics are sketched in 16.2.
 |
While many models operate with a constant dilation, the actual dilation observed in experiments is in fact quite variable. A common approach to describe this variability is to link the current dilation to the current stress ratio . A common stress-dilatancy relations is that of Taylor:
where is the dilation at the ultimate limit state, i.e. for
. With realistic pairs of
and
, the behavior will initially, for low
, be compactive with
. For larger ratios of
and depending on the values of
and
, the behavior may become dilative or remain compactive up to the ultimate limit state. Following Eq.16.5,
can be interpreted in terms of a Mohr-Coulomb dilation angle,
, via the relation
For triaxial compression () we have
It is often observed that and
are quite closely correlated. For sands, the rule of thumb
is often cited.
Alternatively, one may wish to use a constant dilation throughout. The HMC model implemented in OPTUM G2 offers this possibility as well. In that case, the ratio between the plastic volumetric and shear strain rates is simply:
independent of .
On the basis of the preceding discussion, it can be concluded that any credible soil model should involve at least six parameters:
- Two elastic parameters, for example
and
.
- Two strength parameters and a dilation parameter, for example the Mohr-Coulomb
,
and
.
- A ‘fitting parameter’ that reproduces a user specified secant modulus
.
In addition, it is desirable to include pressure dependence into and
. In this is done via two additional parameters: a reference pressure
and an exponent
. The full set of parameters for the HMC model are given below.
Stiffness
The HMC model makes use of three stiffness parameters which can be entered in two different ways, either (Set A):
[MPa] : Young’s modulus in unloading/reloading at reference pressure
.
: Poisson’s ratio in unloading/reloading at reference pressure
.
[MPa] : Secant Young’s modulus in triaxial compression under confining pressure
.
or (Set B):
[MPa] : Shear modulus corresponding to unloading/reloading at reference pressure
.
[MPa] : Bulk modulus corresponding to unloading/reloading at reference pressure
.
[MPa] : Secant shear modulus in triaxial compression under confining pressure
.
It should be noted that while ,
,
and
are true elastic moduli and thus related via the usual elastic relations [
, etc], the elastoplastic secant moduli,
and
, are not related in an obvious linear fashion.
Strength
The strength parameters are the same as for the standard Mohr-Coulomb model:
- c [kPa] : Cohesion.
[
] : Friction angle.
Flow rule
- Flow Rule : Taylor/Constant Dilation
[
] : Dilation angle.
For Flow Rule = Taylor, Taylor’s stress-dilatancy relation Eq.16.17 is used. This implies that the dilation increases as the ultimate limit state is approached. At the ultimate limit state, the dilation is characterized by the angle . In contrast, for Flow Rule = Constant Dilation, the dilation is constant throughout, c.f. Eqn. Eq.16.10.
It is possible to enforce a Dilation Cap following the Mohr-Coulomb material. Once the critical strain is reached (Volumetric or Shear), Flow Rule = Constant Dilation with is enforced.
Pressure dependence
Pressure dependence of the stiffness moduli is included via the following relations:
and
where
with being the minor principal stress. The associated parameters are:
[kPa] : Reference pressure (confining pressure in triaxial compression test).
: Fitting parameter.
The parameter depends on the soil type. For soft clays,
should be chosen as
(giving rise to relations similar to those used in the Modified Cam Clay model) while for sands and other coarse grained materials
is appropriate.
Unit Weights, Initial Conditions, Hydraulic Model
See Section 8.
16.2 Model overview
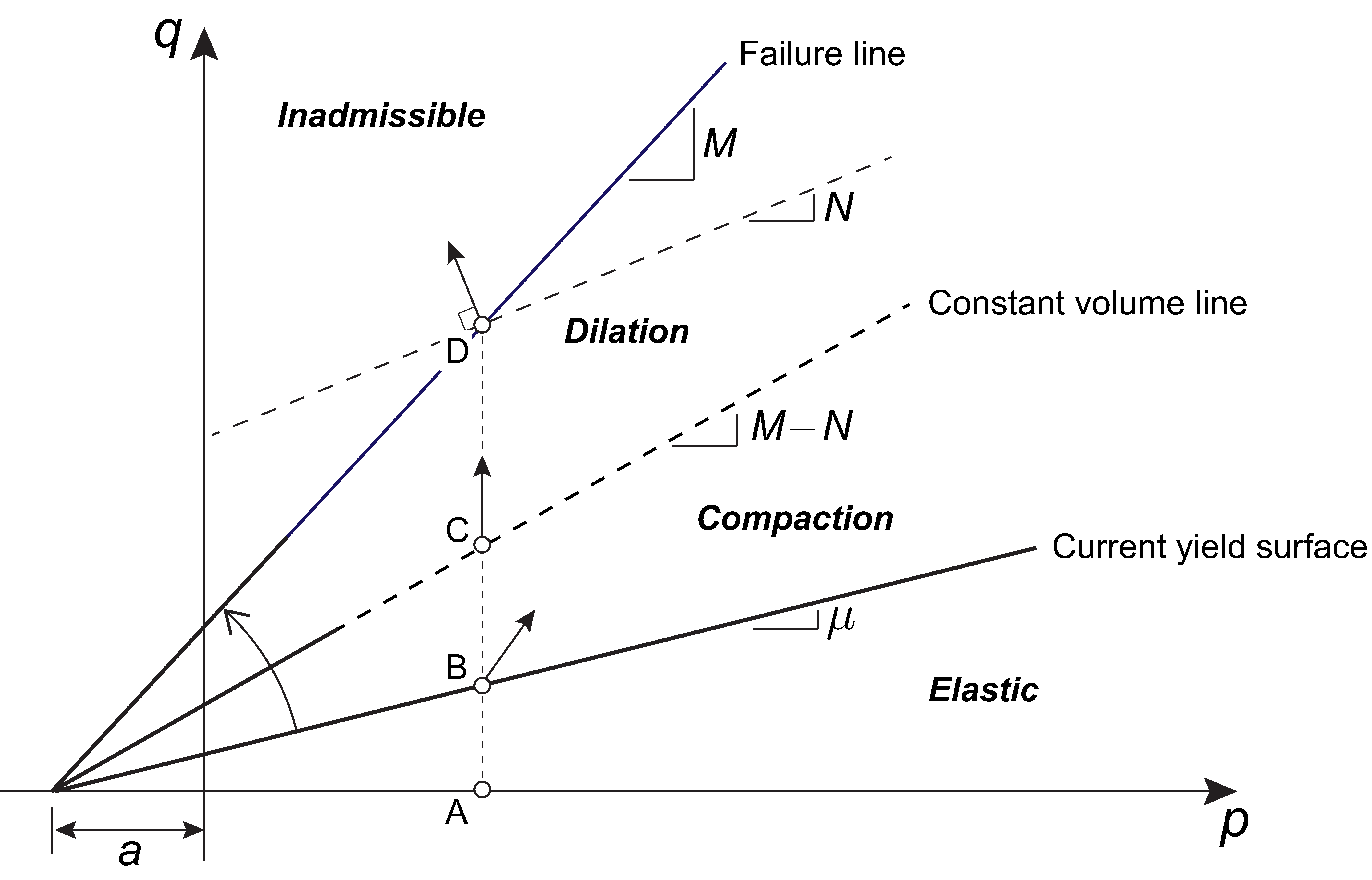 |
The basic premise of the HMC model is sketched in Figure 16.3. In contrast to the standard Mohr-Coulomb model which consists of a single elastic region limited by the failure criterion, the HMC model operates with three regions in –
space:
- An elastic region in which no plastic or otherwise irreversible straining takes place.
- A compaction region where the soil undergoes compaction, i.e. negative dilation.
- A dilation region where the soil undergoes plastic dilation.
Consider an initial stress point as indicated by A in Figure 16.3. Shear loading first implies an initially elastic response up to point B where the initial yield surface is reached. From point A to point B, the yield surface hardens, implying a decrease of stiffness, while the flow rule is such that a compaction takes place. As the loading continues, point C is reached. At this point, the behavior switches from being compactive to being dilative and remains so up to point D at which failure occurs, i.e. the yield surface seizes to harden and remains stationary.
16.2.1 Initial state and small-strain stiffness
In practice, the HMC model is initialized as follows:
- The initial stress state is first calculated on the basis of the specified
. This is either done automatically (if no From stage is specified in Elastoplastic or Multiplier Elastoplastic analysis) or via a separate Initial Stress stage.
- On the basis of the stress state at each point, a parameter
is calculated such that the stress state will satisfy the initial yield criterion
where subscript 0 refers to the initial state.
- Finally, we set
where
is a user defined parameter and use
as the initial yield surface. This means that the initial point will be below yield, i.e.
for
. This situation is sketched in Figure 16.4.
In OPTUM G2, rather than specifying , an equivalent friction angle
is specified under Initial Conditions and the equivalent
calculated by
where is the Lode angle Eq.16.6.
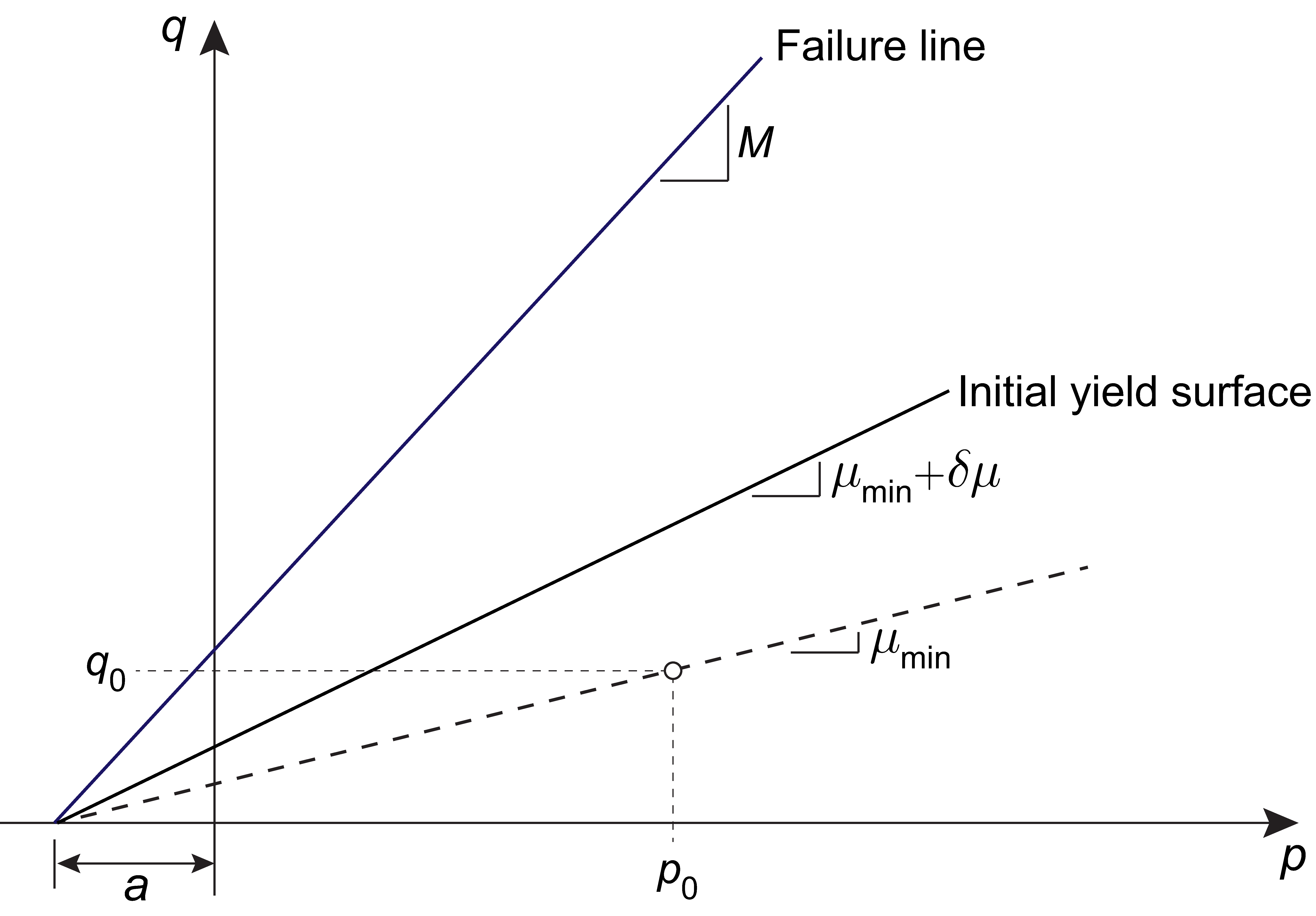 |
 |
The existence of a finite initial elastic range can be correlated to the concept of small-strain stiffness, i.e. the phenomenon that soils at very low levels of strain are much stiffer than at the strain levels usually experienced in standard laboratory tests and in typical boundary value problems. This is discussed in detail by [Wood:1990]Author: D.~{Muir~Wood}
Publisher: Cambridge University Press
Title: Soil Behaviour and Critical State Soil Mechanics
Year: 1990 and [Doherty:2013]Author: J.~P.~Doherty; D.~{Muir Wood}
and [Doherty:2013]Author: J.~P.~Doherty; D.~{Muir Wood}
Journal: Geotechnique
Pages: 661--673
Title: An extended {M}ohr-{C}oulomb ({EMC}) model for predicting the settlement of shallow foundations on sand
Volume: 63
Year: 2013 with respect to the original Extended Mohr-Coulomb model from which the HMC model derives. While the values of
with respect to the original Extended Mohr-Coulomb model from which the HMC model derives. While the values of leading to the desired stiffness degradation with strain is material dependent and must be calibrated in each individual case (from data that normally not is available), the results of [Doherty:2013]Author: J.~P.~Doherty; D.~{Muir Wood}
Journal: Geotechnique
Pages: 661--673
Title: An extended {M}ohr-{C}oulomb ({EMC}) model for predicting the settlement of shallow foundations on sand
Volume: 63
Year: 2013 appear to indicate that a value of
appear to indicate that a value of (together with reasonable values of
and
) may be quite typical.
Some of the experimental results and calibrations presented by [Doherty:2013]Author: J.~P.~Doherty; D.~{Muir Wood}
Journal: Geotechnique
Pages: 661--673
Title: An extended {M}ohr-{C}oulomb ({EMC}) model for predicting the settlement of shallow foundations on sand
Volume: 63
Year: 2013 are shown in Figure 16.5. While these results reveal a rather dramatic degradation of stiffness with shear strain, the effect of small-strain stiffness is for typical boundary value problems (foundations, retaining wall, etc) usually fairly limited.
are shown in Figure 16.5. While these results reveal a rather dramatic degradation of stiffness with shear strain, the effect of small-strain stiffness is for typical boundary value problems (foundations, retaining wall, etc) usually fairly limited.
16.3 Calibration to Erksak sand
The HMC model has been calibrated to drained triaxial tests on Erksak sand at three different densities and at three different confining pressures. In all cases, the reference pressure was set to the default value of kPa. The parameters used are given in Table 16.1 and the resulting fits are shown in Figure 16.6.
| Loose | Medium | Dense | |
|---|---|---|---|
| |
|||
| |
|||
| |
|||
| |
|||
| |
| ||
| |
|||
| Flow Rule | Taylor | Taylor | Taylor |
| |
|
||
| |
|||
| |
 |
16.4 Calibration to Lund sand
A key feature of the HMC model is that the stiffness moduli are pressure dependent. In this way, a set of parameters calibrated under one confining pressure should in principle be valid for all pressures. To verify this assertion, the model is first calibrated to a dense Lund sand under a confining pressure of kPa using
kPa. Simulations are then run for confining pressures of
,
,
and
kPa using the same parameters, including
.
The parameter set and the resulting fits are shown in Table 16.4 and Figure 16.7 respectively. As seen, the model generalizes rather well to both higher and lower pressures than originally calibrated for.
| Flow Rule | Taylor |
 |
16.5 Calibrating  and
and 
The figures below illustrate the relative independence of and
for the Medium sand in Table 16.1. In the figures on the left, the reference unloading/reloading modulus is fixed at
MPa while
is varied between 1/5 to 1/2 of
. This has an immediate effect on the response in loading whereas the response in unloading/reloading is governed solely by
. Conversely, in the figures on the right,
is kept constant at 25 MPa while
is varied from 2 to 5 times
. This has a much less dramatic effect on the results, except in unloading where the stiffness again is governed solely by
.
 |
16.6 Undrained behavior
Under undrained conditions (Drainage Condition = Drained/Undrained in combination with Time Scope = Short Term), the overall behaviour depends on a combination of the strength and stiffness parameters. In particular, for a dilation angle of , the excess pore pressures will increases indefinitely resulting in an infinite strength (unless a cavitation cut-off is introduced in which case the strength will be finite). Conversely, for
, the strength will eventually decrease to zero corresponding to static liquefaction. For the special case of
, the strength is finite and depends on a combination of the strength and stiffness parameters. An example of the influence of the dilation angle on the overall response is shown in Figure 16.9.
 |
16.7 Governing equations
In the following, the governing equations of the HMC model are briefly summarized.
The basic premise of the HMC model is sketched in Figure 16.3. The current mobilized strength is characterized by the line where
is the current mobilized friction coefficient and
is an attraction (tensile strength). As hardening proceeds, i.e. as
increases, the constant volume line
is reached. At this state, the dilation is zero. Hardening progresses further until
at which point the material behaves in a perfectly plastic manner with dilation coefficient
.
To capture this behaviour, and to account for elastic unloading, a hardening yield surface is introduced. This is given by
What remains is to specify an appropriate flow rule that leads to the behaviour described above and to construct a hardening rule that prevents any further hardening of the yield surface at .
Concerning the former, an appropriate plastic potential is [Wood:2004]Author: D.~{Muir Wood}
Publisher: Cambridge University Press
Title: Geotechnical Modelling
Year: 2004 , [Doherty:2013]Author: J.~P.~Doherty; D.~{Muir Wood}
, [Doherty:2013]Author: J.~P.~Doherty; D.~{Muir Wood}
Journal: Geotechnique
Pages: 661--673
Title: An extended {M}ohr-{C}oulomb ({EMC}) model for predicting the settlement of shallow foundations on sand
Volume: 63
Year: 2013 :
:
where should be chosen such that
passes through the current stress point, i.e.
. This plastic potential implies the stress-dilatancy relation of Taylor:
where and
are the plastic volumetric and shear strains respectively.
Secondly, the stress ratio in elastoplastic loading is assumed to depend on the plastic shear strain as:
where is a model parameter. We note that
in fact is the plastic shear strain at half the ultimate stress ratio. The incremental form of the above leads to the hardening rule:
where it is evident that hardening terminates at . The above hardening rule generally leads to stress-strain curves similar to those observed experimentally.
Finally, the behaviour within the elastic domain is based on linear elasticity:
16.7.1 Pressure dependence
The version of the HMC model implemented in OPTUM G2 differs from the original model in two ways.
Firstly, the elastic moduli are pressure dependent following Eq.16.11.
Secondly, the hardening parameter is adjusted to reproduce the user specified secant moduli,
or
. With
specified, the expression for
is:
while the expression consistent with a user specified is:
where and
are pressure dependent following Eq.16.12. We note that for
,
becomes constant in the special case where the pressure remains constant and equal to the minor principal stress. In that case, the original HMC model of [Wood:2004]Author: D.~{Muir Wood}
Publisher: Cambridge University Press
Title: Geotechnical Modelling
Year: 2004 is recovered exactly.
is recovered exactly.
16.8 Incremental stress-strain relations
Assuming that the initial stress is at the yield surface (), the incremental stress-strain relations for triaxial compression are given by
where
with
and
16.9 Limit Analysis and Strength Reduction
Limit Analysis and Strength Reduction are carried out using equivalent Mohr-Coulomb parameters. The resulting limit loads may differ somewhat from those of a full elastoplastic analysis. Under drained conditions, the difference is due to the effects of nonassociativity. The same observations as for the standard Mohr-Coulomb model here apply. In particular, limit loads may be estimated using Davis parameters (see Section 8.13).
For undrained analysis, similar observations hold. The HMC plastic potential is essentially of the Drucker-Prager type and thus differs slightly from that used in the standard Mohr-Coulomb model. However, for the constant mean effective stress conditions that exist under undrained conditions, the effect on the bearing capacity is much less than under drained conditions.
16.10 Variational model
The HMC model implemented in is based on the incremental variational plasticity framework proposed by [Krabbenhoft:2007IJSS]Author: K.~Krabbenhoft; A.~V.~Lyamin; S.~W.~Sloan
Journal: International Jounal of Solids and Structures
Pages: 1533-1549
Title: Formulation and solution of some plasticity problems as conic programs
Volume: 44
Year: 2007 [see also [Krabbenhoft:2012IJNME]Author: K.~Krabbenhoft; M.~R.~Karim; A.~V.~Lyamin; S.~W.~Sloan
[see also [Krabbenhoft:2012IJNME]Author: K.~Krabbenhoft; M.~R.~Karim; A.~V.~Lyamin; S.~W.~Sloan
Journal: International Journal for Numerical Methods in Engineering
Pages: 1089--1117
Title: Associated computational plasticity schemes for nonassocited frictional materials
Volume: 89
Year: 2012 , [Krabbenhoft:2012CMAME]Author: K.~Krabbenhoft; A.~V.~Lyamin
, [Krabbenhoft:2012CMAME]Author: K.~Krabbenhoft; A.~V.~Lyamin
Journal: Computer Methods in Applied Mechanics and Engineering
Pages: 239--249
Title: Computational {C}am clay plasticity using second-order cone programming
Volume: 209--212
Year: 2012 ]. This framework allows for the construction of models with arbitrary flow rules while maintaining the basic features of associated plasticity, notably a symmetric elastoplastic tangent modulus.
]. This framework allows for the construction of models with arbitrary flow rules while maintaining the basic features of associated plasticity, notably a symmetric elastoplastic tangent modulus.
The model is constructed as follows. Consider an evolutionary process and assume that an estimate () of the stress and hardening variables is available. Next, introduce the following yield function:
As , this reduces to the original yield function Eq.16.15.
The plastic strain rates follow from the associated flow rule:
Setting
and letting reproduces Taylor’s stress-dilatancy relation Eq.16.17.
Finally, the hardening rule is specified as
which again approaches the original hardening rule Eq.16.19 as .
16.11 Extension to general stress space
Extension of the basic -
formulation to general stress space can be achieved by replacing
and
with equivalent Lode’s angle dependent quantities,
and
respectively:
where is Lode’s angle.
16.11.1 Optimization
The incremental elastoplastic problem is given by
where the yield function is given by
with
to reproduce Taylor’s dilation rule.
The hardening modulus is given by
An effective averaging scheme is
where subscripts and
refer to the last determined and new states respectively.
17 LINEAR ELASTIC
The Linear Elastic material type implements Hooke’s law and does not involve any limitations on the strength in the form of yield conditions or similar. All other properties – Drainage, Stiffness, Unit Weights, Initial Conditions, and Hydraulic Model are as for the Mohr-Coulomb material (see Section 8).
18 RIGID
The Rigid material type describes a perfectly rigid and infinitely strong material. Its only properties – Drainage, Unit Weights, and Hydraulic Model are as for the Mohr-Coulomb material (see Section 8). The Rigid material is convenient for the modeling of foundations, retaining walls and similar structures provided that one is confident that the failure as well as the majority of the deformations take place elsewhere.
19 FLUIDS
In OPTUM G2, Fluids are special cases of Solids. Internally, they are modeled as elastoplastic Solids capable of sustaining an indefinite amount of hydrostatic compression and no shear stress. The elastic parameter is the bulk modulus . Internally, Poisson’s ratio is chosen to balance the requirement that the material should be incompressible (
) together the requirement that the Young’s modulus
should remain finite. The only other material parameter is the unit weight,
. For the default material Water, the parameters are
MPa and
kN/m
corresponding to water under standard atmospheric conditions. Furthermore, Fluids are assigned an artificial hydraulic conductivity of 1,000 times the largest hydraulic conductivity used in the stage for any Soild material.
20 PLATES
Plates are structural elements used to model elements whose thickness is sufficiently small to be negligible compared to the overall problems dimensions. Common examples are foundation plates and sheet pile walls. Plates may also be useful in a number of other situations to model objects whose overall properties are not well defined other than they are very stiff (or very flexible) compared to the surrounding solid materials. Two types of Plates are available: Plate and Rigid Plate.
20.1 Plate
The material type Plate is an elastoplastic plate which in plane strain is equivalent to a standard Euler-Bernoulli beam.
The model parameters can be entered in two different formats referred to as Parameter Sets A and B respectively. These are shown in Figure 20.1 which also summarizes the relation between the parameters of the different sets.
 |
The two sets share two properties: Yield Envelope and Permeable (Yes/No). The latter setting concerns Seepage analysis and determines whether the plate will be considered as an impermeable barrier or a fully permeable boundary between two solids. Note that the Permeable setting is a material setting and relates to all plates assigned the material in all stages.
Regarding the yield envelope, two options are available. Square (the default setting) imposes the following yield criterion:
A more conservative estimate of the strength of the wall may be realized by use of the Diamond yield criterion:
The two yield criteria are shown in Figure 20.2. Usually, the difference in results between the two criteria is relatively minor as most problems relevant to geotechnics tend to be dominated by bending.
 |
20.2 Rigid Plate
The Rigid Plate material type is a special case of the material described above. It involves only two parameters: weight and Permeable (Yes/No). This element is convenient in cases where the exact properties of the actual plate are not well defined, but where it can be assumed that it has a much higher strength and stiffness than the surrounding material.
20.3 Additional features
Plates may be assigned interface materials from the Solids category and hinges which in themselves require a set of material parameters (see Section 23). Both these additional features may be accessed and edited via the property window by selecting a given plate. An example is shown in Figure 20.3.
 |
OPTUM G2 offers two possibilities for defining the Reduction Factor, , used to modify the interface strength parameters. These may be set under Physical Parameters in Project (see Figure 20.4). For the Mohr-Coulomb model, the default option “c, phi” reduces the cohesion and friction angle by the factor
. This follows many codes of practice including Eurocode 7. The second option “c, tan(phi)” reduces
and
by the specified factor
. The rules for other models are given in the table below.
 |
| Original | Reduced Parameters | Reduced Parameters | |
| Parameters | Option = c, phi | Option = c, tan(phi) | |
| Mohr-Coulomb | |||
| Drucker-Prager | |||
| Tresca (Standard) | |||
| Tresca (Generalized) | |||
| AUS | |||
| Hoek-Brown | |||
| GSK | |||
| Bolton | |||
| Modified Cam Clay | |||
| HMC |
21 GEOGRIDS
Geogrids are similar to Plates, but cannot sustain uniaxial compression and offer no resistance to bending. As such, the material parameters concern only the tensile stiffness and strength (see Figure 21.1). Geogrids are considered weightless and may be either fully permeable or impermeable.
 |
Besides geogrids, geotextiles, thin membranes, etc, Geogrid elements can also be used to account for grouting in connection with soil anchors (see the Examples Manual).
As for Plates (see the previous section), it it possible to assign arbitrary Solid materials to the interfaces of Geogrids and to apply a strength reduction factor .
22 CONNECTORS
Materials in the Connectors category can be assigned to Connectors and Fixed End Anchors. Connectors are one-dimensional truss elements that do not interact with the solid domain. In other words, they may be viewed as existing in a layer outside the solid domain. These elements are commonly used to account for anchoring systems. As for Geogrids, Connectors can only sustain normal forces. The material parameters can be entered via two Parameter Sets as shown in Figure 22.1. All parameters refer to the individual rods. Similar, the results reported are for the individual Connectors.
 |
23 HINGES
Hinges can be applied at the end of plates (see Section 20). These are elastoplastic elements defined by two material parameters:
- Rotational Stiffness,
(kNm/m/rad)
- Yield Moment,
(kNm/m)
The moment-rotation behavior of Hinge elements is shown in Figure 23.1. For moments , the mutual rotation of the Plates on either side of the hinge is given by
For moments , the hinge behaves in a perfectly plastic manner with zero rotational stiffness.
The default settings, and
, thus correspond to a standard hinge not offering any resistance to rotation. Similarly, for
a standard rigid connection is reproduced.
 |
24 PILE ROWS
While the rigorous modeling of piles subjected to arbitrary loading (lateral, axial, moment) requires a full three-dimensional analysis, a number of special cases can be handled in two spatial dimensions. A single pile subjected to axial loading can be modeled as an axisymmetric structure. Furthermore, a pile row subjected to more general loading can be modeled using a Plate element in an plane strain analysis – provided the spacing between the piles is sufficiently small for the row to behave more or less as a monolithic structure.
The case of pile row with a spacing in the order of several pile diameters is more challenging to model. On one hand, the individual piles interact with the soil in much the same way as a Plate element. On the other hand, the soil may flow between the piles. Indeed, if the spacing is sufficiently large, part of the soil between the piles will unaffected by the pile movement.
The Pile Row feature available in OPTUM G2 attempts to cater for this partial interaction between the piles and the soil. Following [Sluis:2014]Author: J.~M.~M.~Sluis; F.~Besseling; P.~H.~H.~Stuurwold
Booktitle: Numerical Methods in Geotechnical Engineering
Pages: 277--282
Publisher: Taylor \& Francis
Title: Modelling of a pile row in a 2{D} plane strain {FE}-analysis
Year: 2014 , the basic idea is to consider the soil and the piles as being located in two different ‘layers’ similar to what is the case with Connectors. However, while Connectors have no interaction with the soil at all, the piles in a Pile Row are connected to the soil by means of springs, the properties of which imply more or less of an interaction. The principle is sketched in Figure 24.1.
, the basic idea is to consider the soil and the piles as being located in two different ‘layers’ similar to what is the case with Connectors. However, while Connectors have no interaction with the soil at all, the piles in a Pile Row are connected to the soil by means of springs, the properties of which imply more or less of an interaction. The principle is sketched in Figure 24.1.
 |
Three different types of springs, accounting for three different types of interaction are considered: axial (A) for interaction in the direction of the pile, lateral (L) for interaction perpendicular to the pile, and base (B) for interaction between the soil and the base of the piles in the row. The interaction springs all have a finite strength. In the following, the parameters associated with Pile Rows are discussed in detail.
24.1 Piles
The pile of the Pile Row are modeled using standard beam elements. The input parameters are those of the individual piles. Three different types of piles requiring input of the specific dimensions are available: Massive Circular, Circular Tube, and Massive Square. In addition, the cross section area and moment of inertia for a pile with an arbitrary cross section can be entered via the User option. The different parameter sets are shown in Figure 24.2.
 |
24.2 Soil-Pile Stiffness
 |
Following, [Sluis:2014]Author: J.~M.~M.~Sluis; F.~Besseling; P.~H.~H.~Stuurwold
Booktitle: Numerical Methods in Geotechnical Engineering
Pages: 277--282
Publisher: Taylor \& Francis
Title: Modelling of a pile row in a 2{D} plane strain {FE}-analysis
Year: 2014 , the stiffness of the springs connecting the pile and the soil are calculated as:
, the stiffness of the springs connecting the pile and the soil are calculated as:
where ,
and
are the axial, lateral and base springs respectively,
are interaction factors and
is the shear modulus of the soil. [Sluis:2014]Author: J.~M.~M.~Sluis; F.~Besseling; P.~H.~H.~Stuurwold
Booktitle: Numerical Methods in Geotechnical Engineering
Pages: 277--282
Publisher: Taylor \& Francis
Title: Modelling of a pile row in a 2{D} plane strain {FE}-analysis
Year: 2014 suggests the following interaction factors:
suggests the following interaction factors:
These are the interaction factors implemented with the Default option (see Figure 24.3). Alternatively, the interaction factors or the spring stiffnesses can be entered manually.
24.3 Soil-Pile Strength
All the interaction springs have a finite strength that can be specified as shown in Figure 24.4. The base spring cannot sustain tension.
 |
24.4 Additional properties
24.5 Base
For a given Pile Row segment, the base can either be specified as being located at the end (E) of the beginning (B) of the segment (see Figure 24.5). Alternatively, None specifies that no base stiffness and strength are available. A Pile Row base is denoted by a gray arrow as shown in Figure 24.5.
 |
24.6 Elastic Zone
Following [Sluis:2014]Author: J.~M.~M.~Sluis; F.~Besseling; P.~H.~H.~Stuurwold
Booktitle: Numerical Methods in Geotechnical Engineering
Pages: 277--282
Publisher: Taylor \& Francis
Title: Modelling of a pile row in a 2{D} plane strain {FE}-analysis
Year: 2014 , the elements in a finite zone around the pile are assumed to be elastic. By default, the width of this elastic zone is
, the elements in a finite zone around the pile are assumed to be elastic. By default, the width of this elastic zone is (see Figure 24.6).
 |
A user defined width of the elastic zone can be set by selecting User under Elastic Zone. Alternatively, no elastic zone is included by selecting None.
25 NAIL ROWS
Nail Rows are as special case of Pile Rows corresponding to the settings shown in Figure 25.1. The user input are: Nail Diameter (cm), Young’s Modulus (MPa), Spacing (m), and Axial and Lateral Strengths (kN/m) along the Nail. The base strength is zero while the lateral strength is unlimited, implying failure of the surrounding soil rather than in the springs connecting the Nail to the soil. Finally, in contrast to Piles, no elastic zone around the Nail is considered.
 |
Back to OPTUM G2 main page
REFERENCES
| [Alshibli:2003] | K.~A.~Alshibli; S.~N.~Batiste; S.~Sture (2003): Strain Localization in Sand: Plane Strain versus Triaxial Compression. Journal of Geotechnical and Geoenvironmental Engineering, 129, 483--494 |  |
| [Andersen:2013] | K.~H.~Andersen; K.~Schjetne (2013): Database of Friction Angles of Sand and Consolidation Characteristics of Sand, Silt, and Clay. Journal of Geotechnical and Geoenvironmental Engineering, 139, 1140-1155 |  |
| [Bolton:1986] | M.~D.~Bolton (1986): The strength and dilancy of sands. Geotechnique, 36, 65--78 |  |
| [Borja:1985] | R.~I.~Borja; E.~Kavazanjian (1985): A constitutive model for the stress-strain-time behaviour of `wet clays'. Geotechnique, 35, 283--298 |  |
| [Burland:1996] | J.~B.~Burland; S.~Rampello; V.~N.~Georgiannou; G.~Calabresi (1996): A laboratory study of the strength of four stiff clays. Geotechnique, 146, 491--514 |  |
| [Davis:1968] | E.~H.~Davis (1968): Theories of plasticity and the failure of soil masses. %publisher%, Soil Mechanics: Selected Topics |  |
| [Davis:1980] | E.~H.~Davis (1980): Some plasticity solutions relevant to the bearing capacity of rock and fissured clay. %publisher%, Proc. 3rd A.N.Z. Conf. on Geomechanics, vol. 3. Wellington, New Zealand |  |
| [Doherty:2013] | J.~P.~Doherty; D.~{Muir Wood} (2013): An extended {M}ohr-{C}oulomb ({EMC}) model for predicting the settlement of shallow foundations on sand. Geotechnique, 63, 661--673 |  |
| [Gercek:2007] | H.~Gercek (2007): Poisson's ratio values for rocks. International Journal of Rock Mechanics and Mining Sciences, 44, 1--13 |  |
| [Ghan:2010] | B.~Ghanbarian-Alavijeh; A.~Liaghat; G.~H.~Huang; M.~T~van~Genuchten (2010): Estimation of the van Genuchten Soil Water Retention Properties from Soil Textural Data. Pedosphere, 20, 456--465 |  |
| [Graham:1983] | J.~Graham; G.~T.~Houlsby (1983): Anisotropic elasticity of a natural clay. Geotechnique, 33, 165--180 |  |
| [Hara:1974] | A.~Hara; T.~Otha; M.~Niwa; S.~Tanaka; T.~Banno (1974): Shear modulus and shear strength of cohesive soils. Soils and Foundations, 14, 1--12 |  |
| [HoekBook:2007] | E.~Hoek (2007): Practical Rock Engineering. (%edition%). %publisher%, %address%, %pages% |  |
| [Karlsrud:2013] | K.~Karlsrud; F.~G.~Hernandez-Martinez (2013): Strength and deformation properties of Norwegian clays from laboratory tests on high-quality block samples1. Canadian Geotechnical Journal, 50, 1273--1293 |  |
| [Krabbenhoft:2007IJSS] | K.~Krabbenhoft; A.~V.~Lyamin; S.~W.~Sloan (2007): Formulation and solution of some plasticity problems as conic programs. International Jounal of Solids and Structures, 44, 1533-1549 |  |
| [Krabbenhoft:2012CMAME] | K.~Krabbenhoft; A.~V.~Lyamin (2012): Computational {C}am clay plasticity using second-order cone programming. Computer Methods in Applied Mechanics and Engineering, 209--212, 239--249 |  |
| [Krabbenhoft:2012IJNME] | K.~Krabbenhoft; M.~R.~Karim; A.~V.~Lyamin; S.~W.~Sloan (2012): Associated computational plasticity schemes for nonassocited frictional materials. International Journal for Numerical Methods in Engineering, 89, 1089--1117 |  |
| [Krenk:2000b] | A.~Ahadi; S.~Krenk (2000): Characteristic state plasticity for granular materials. {P}art {II}: {M}odel calibration and results. International Journal of Solids and Structures, 37, 6361--6380 |  |
| [Ladd:1991] | C.~C.~Ladd (1991): Stability evaluation during staged construction. Journal of Geotechnical Engineering, 117, 540--615 |  |
| [Ladd:2003] | C.~C.~Ladd; D.~J.~{D}e{G}root (2003): Recommended practice for soft ground site characterization: {A}rthur {C}asagrande {L}ecture. %publisher%, Proceedings of the 12th Panamerican Conference on Soil Mechanics and Geotechnical Engineering, Cambridge, MA |  |
| [Larsson:1980] | R.~Larsson (1980): Undrained shear strength in stability calculation of embankments and foundations on soft clays. Canadian Geotechnical Journal, 17, 591--602 |  |
| [Mesri:1975] | G.~Mesri (1975): Discussion of "{N}ew design procedure for stability of soft clays" by {L}add, {C. C.} and {F}oott, {R.}. Journal of the Geotechnical Engineering Division, 101, 409--412 |  |
| [Mesri:1986] | G.~Mesri; A.~Castro (1986): ${C}_\alpha/{C}_c$ concept and ${K}_0$ during secondary compression. Journal of Geotechnical Engineering, 113, 230--247 |  |
| [Potts:2001] | D.~M.~Potts; L.~Zdravkovic (2001): Finite Elements Analysis in Geotechnical Engineering. (%edition%). Thomas Telford, %address%, %pages% |  |
| [Roscoe:1968] | K.~H.~Roscoe; J.~B.~Burland (1968): On the generalized stress-strain behaviour of wet clay. Cambridge University Press, Engineering Plasticity |  |
| [SK:2012] | S.~Krabbenhoft; J.~Clausen; L.~Damkilde (2012): The Bearing Capacity of Circular Footings in Sand: Comparison betweenModel Tests and Numerical Simulations Based on a Nonlinear {M}ohr Failure Envelope. Advances in Civil Engineering, Article ID: 947276, 1--10 |  |
| [Schofield:1968] | A.~Schofield; P.~Wroth (1968): Critical State Soil Mechanics. (%edition%). Cambridge University Press, %address%, %pages% |  |
| [Skempton:1957] | A.~.W.~Skempton (1957): Discussion: The planning and design of the new {H}ong {K}ong airport. Proceedings of the Institution of Civil Engineers London, 7, 305--307 |  |
| [Sluis:2014] | J.~M.~M.~Sluis; F.~Besseling; P.~H.~H.~Stuurwold (2014): Modelling of a pile row in a 2{D} plane strain {FE}-analysis. Taylor \& Francis, Numerical Methods in Geotechnical Engineering |  |
| [Stakemann:1976] | O.~Stakemann (1976): Brudbetingelse for {G12}-sand og plane modelfors�g ({F}ailure conditions for {G12}-sand and plane strain model tests). Internal Memo I.M. 1976-1, Danish Geotechnical Institute. |  |
| [Vardenega:2011] | P.~J.~Vardanega; M.~D.~Bolton (2011): Strength mobilization in clays and silts. Canadian Geotechnical Journal, 2048, 1485--1503 |  |
| [White:2008] | D.~J.~White; K.~L.~Teh; C.~F.~Leung; Y.~K.~Chow (2008): A comparison of the bearing capacity of flat and conical circular foundations on sand. Geotechnique, 58, 781--792 |  |
| [Wood:1990] | D.~{Muir~Wood} (1990): Soil Behaviour and Critical State Soil Mechanics. (%edition%). Cambridge University Press, %address%, %pages% |  |
| [Wood:2004] | D.~{Muir Wood} (2004): Geotechnical Modelling. (%edition%). Cambridge University Press, %address%, %pages% |  |
| [Yu:2006Book] | H.~S.~Yu (2006): Plasticity and Geotechnics. (%edition%). Springer-Verlag, %address%, %pages% |  |
| [Zheng:1997] | Z.~Zheng; J.~R.~Booker; J.~P.~Carter (1997): Limit analysis of the bearing capacity of Fissured materials. International Journal of Solids and Structures, 37, 1211--1243 |  |